Đáp án C
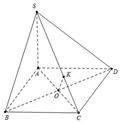
Gọi O là tâm hình vuông ABCD ta có:
A C ⊥ B D B D ⊥ S A ⇒ B D ⊥ S A C
Dựng O K ⊥ S C ⇒ O K là đoạn vuông góc chung của BD và SC
Khi đó d B D ; S C = O K = 1 2 d A ; S C = 1 2 S A . A C S A 2 + A C 2
Với A C = a 2 ⇒ d = a 6 6 .
Đáp án C

Gọi O là tâm hình vuông ABCD ta có:
A C ⊥ B D B D ⊥ S A ⇒ B D ⊥ S A C
Dựng O K ⊥ S C ⇒ O K là đoạn vuông góc chung của BD và SC
Khi đó d B D ; S C = O K = 1 2 d A ; S C = 1 2 S A . A C S A 2 + A C 2
Với A C = a 2 ⇒ d = a 6 6 .
Cho hình lập phương ABCD.A’B’C’D’. Mặt phẳng (BDC’) chia khối lập phương thành 2 phần. Tính tỉ lệ giữa phần nhỏ và phần lớn:
A. 5 6
B. 1 5
C. 1 3
D. 1 6
Cho hình lập phương ABCD.A' B'C' D' cạnh bằng a và K là một điểm nằm trên cạnh CC’ sao cho C K = 2 a 3 . Mặt phẳng α qua A, K và song song với BD chia khối lập phương thành hai phần có thể tích V 1 , V 2 V 1 < V 2 . Tính tỉ số V 1 V 2
A. V 1 V 2 = 1 4
B. V 1 V 2 = 1 2
C. V 1 V 2 = 2 3
D. V 1 V 2 = 1 3
Cho hình lập phương ABCD.A’B’C’D’. I là trung điểm BB’. Mặt phẳng (DIC’) chia khối lập phương thành 2 phần có tỉ số thể tích phần bé chia phần lớn bằng:
A. 1:3
B. 7:17
C. 4:14
D. 1:2
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Các điểm E và F lần lượt là trung điểm của C'B' và C'D'. Mặt phẳng ( AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể
tích khối chứa điểm A' và V 2 là thể tích khối chứa điểm C’. Khi đó tỉ số V 1 V 2 bằng
A. 25 47
B. 1
C. 17 25
D. 8 17
Cho hình chóp tứ giá đều S.ABCD có cạnh đáy bằng a, cạnh bên hợp với đáy một góc 60 ° . Gọi M là điểm đối xứng của C qua D, N là trung điểm SC. Mặt phẳng (BMN) chia khối chóp S.ABCD thành hai phần. Tỉ số thể tích giữa hai phần (phần lớn trên phần bé) bằng:
A. 7 5
B. 1 7
C. 7 3
D. 6 5
Trong không gian với hệ toạ độ Oxyz, cho tứ diện ABCD với A(3;5;-1),B(0;-1;8),C(-1;-7;3),D(1;0;2) và điểm M(1;1;5). Mặt phẳng (P):ax+by+cz-14=0 qua hai điểm D,M cắt cạnh AC và (P) chia khối tứ diện ABCD thành hai phần có thể tích bằng nhau. Giá trị của biểu thức a+b+c bằng
A. 10
B. 16
C. 8
D. -36
Cho hình chóp cụt ABC.A′B′C′ có hai đáy ABC và A′B′C′ có diện tích lần lượt là S 1 và S 2 . Mặt phẳng (ABC′) chia hình chóp cụt thành hai phần, Tính tỉ số thể tích hai phần đó.
A. S 2 S 1 + S 1 S 2
B. S 1 S 2 + S 1 S 2
C. S 1 S 2 − S 1 S 2
D. S 2 S 1 − S 1 S 2
Người ta cắt đôi đoạn dây thép dài 10m thành hai phần. Phần 1 lại cắt thành 6 phần bằng nhau và ghép thành một hình tứ diện, phần 2 lại cắt thành 12 phần bằng nhau và ghép thành một hình lập phương sao cho tổng diện tích xung quanh của hai hình là nhỏ nhất.
Gọi a là độ dài cạnh của hình tứ diện, b là độ dài cạnh của hình lập phương thì a + b là:
A. 5 + 5 3 3
B. - 5 + 5 3 3
C. - 5 + 20 3 3
D. 5 + 20 3 3
Cho khối lập phương ABCD.A’B’C’D’ cạnh a. Các điểm E, F lần lượt là trung điểm của C’B’ và C’D’ . Mặt phẳng (AEF) cắt khối lập phương đã cho thành hai phần, gọi V 1 là thể tích khối chứa điểm A' và V 2 là thể tích khối chứa điểm C'. Khi đó V 1 V 2 là:
A. 25 47
B. 1
C. 2
D. 3