Đáp án A
Gọi P là trung điểm cùa DD'
A'B'NP là hình bình hành => A'P // B'N
A'PDM là hình bình hành => A'P // MD
=> B'N // MD hay B' M, N, D đồng phẳng.
Tứ giác B'NDM là hình bình hành.
Có DM = B'M nên B'NDM là hình thoi.

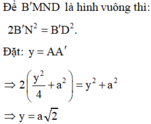
Đáp án A
Gọi P là trung điểm cùa DD'
A'B'NP là hình bình hành => A'P // B'N
A'PDM là hình bình hành => A'P // MD
=> B'N // MD hay B' M, N, D đồng phẳng.
Tứ giác B'NDM là hình bình hành.
Có DM = B'M nên B'NDM là hình thoi.

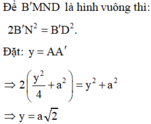
Cho lăng trụ đứng A B C D . A ' B ' C ' D ' có đáy là hình thoi cạnh a, góc B A D ^ = 60 ° ; A A ' = a 2 . M là trung điểm của AA’ . Gọi φ của góc giữa hai mặt phẳng ( B ' M D và A B C D . Khi đó c os φ bằng:
A. 3 3
B. 3 4
C. 2 3
D. 5 3
Cho lăng trụ ABCD.A'B'C'D' có đáy ABCD là hình thoi, A C = 2 a , B A D ^ = 120 ∘ . Hình chiếu vuông góc của điểm B trên mặt phẳng A ' B ' C ' D ' là trung điểm cạnh A' B' góc giữa mặt phẳng A C ' D ' và mặt đáy lăng trụ bằng 60 ∘ . Tính thể tích V của khối lăng trụ A B C D . A ' B ' C ' D '
A. V = 2 3 a 3
B. V = 3 3 a 3
C. V = 3 a 3
D. V = 6 3 a 3
Cho hình lăng trụ ABCD.A'B'C'D' có đáy là hình thoi cạnh bằng a và A B C ⏜ = 120 ° . Góc giữa cạnh bên AA' và mặt đáy bằng 60 ° , điếm A’ cách đều các điểm A, B, D . Tính thể tích khối lăng trụ đã cho theo a.
A. a 3 3 3
B. a 3 3 2
C. a 3 3 12
D. a 3 3 6
Cho hình lăng trụ đứng ABCD . A ' B ' C ' D ' có đáy là hình vuông cạnh a và chiều cao AA ' = 3 a . Trên CC' lấy điểm M, trên DD' lấy điểm N sao cho C ' M = 2 MC và DN = 2 ND ' . Tính cosin góc giữa hai mặt ( B ' MN ) và (ABCD).
A . 1 3 .
B. 1 2
C. 1 6
D. 2 6
Cho hình lăng trụ A B C D . A ' B ' C ' D ' có đáy ABCD là hình thoi cạnh a, tâm O và A B C = 120 ° . Các cạnh AA', A'B, A' D cùng tạo với đáy một góc 60 ° .Tính theo a thể tích V của khối lăng trụ đã cho.
A. a 3 3
B. a 3 3 6
C. a 3 3 2
D. 3 a 3 2
Cho hình lăng trụ đều ABCD.A’B’C’D’ có đáy là hình vuông cạnh a. Mặt phẳng (α) lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng (α) và mặt phẳng (ABCD) là 600. Diện tích tứ giác MNPQ là :
A. 2 3 a 2
B. 1 2 a 2
C. 2 a 2
D. 3 2 a 2
Cho hình lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạnh a, tam giác A' BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), M là trung điểm cạnh CC'. Tính cosin góc α giữa hai đường thẳng AA' và BM.
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a; tam giác A’BC đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABC) M là trung điểm của cạnh CC’. Tính cosin góc α là góc giữa hai đường thẳng AA’ và BM
A. cos α = 2 22 11
B. cos α = 11 11
C. cos α = 33 11
D. cos α = 22 11
Cho hình lăng trụ tam giác A B C . A ' B ' C ' có đáy là tam giác ABC vuông tại A, A B = 3 , A C = 4 và A A ' = 61 2 . Hình chiếu của B’ lên mặt phẳng A B C là trung điểm cạnh BC, điểm M là trung điểm cạnh A ' B ' . Tính cosin của góc tạo bởi hai mặt phẳng A M C ' và (A’BC) bằng:
A. 11 3157 .
B. 13 65 .
C. 33 3517 .
D. 33 3157 .