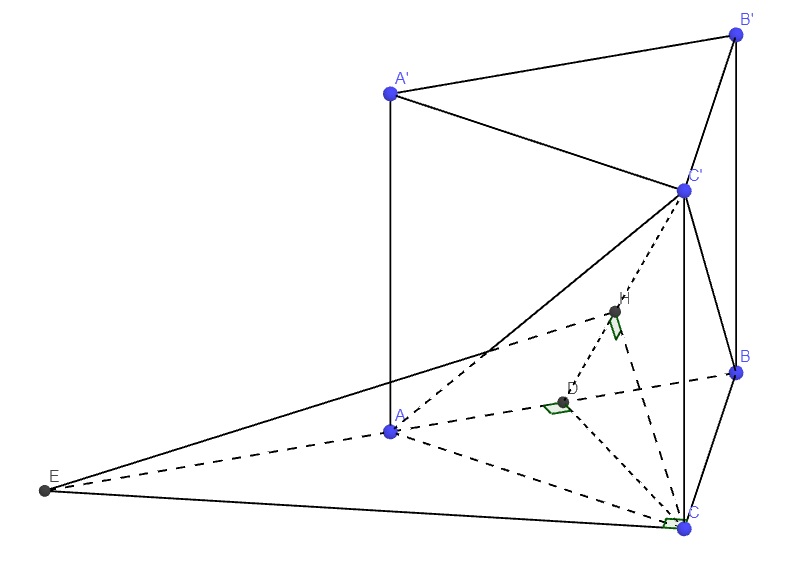
Gọi D là trung điểm AB
Trong mp (CDC'), từ C kẻ \(CH\perp C'D\)
Do lăng trụ đều \(\Rightarrow\Delta ABC\) đều \(\Rightarrow CD\perp AB\Rightarrow AB\perp\left(CDC'\right)\)
\(\Rightarrow AB\perp CH\)
\(\Rightarrow CH\perp\left(ABC'\right)\Rightarrow CH=d\left(C;\left(ABC'\right)\right)=2a\)
Trong mp (ABC), qua C kẻ đường thẳng vuông góc BC cắt AB kéo dài tại E
\(CC'\perp\left(ABC\right)\) (lăng trụ đều) \(\Rightarrow CC'\perp EC\)
\(\Rightarrow EC\perp\left(BCC'B'\right)\)
\(\Rightarrow\widehat{ECH}\) là góc giữa (ABC') và (BCC'B')
Do \(CH\perp\left(ABC'\right)\Rightarrow CH\perp EH\Rightarrow\Delta CEH\) vuông tại H
\(\Rightarrow cos\alpha=cos\widehat{ECH}=\dfrac{CH}{EC}=\dfrac{1}{2\sqrt{3}}\)
\(\Rightarrow EC=2\sqrt{3}CH=4a\sqrt{3}\)
Tam giác BCE vuông tại C \(\Rightarrow\widehat{E}=90^0-\widehat{B}=30^0\)
\(\Rightarrow CD=EC.sin\widehat{E}=2a\sqrt{3}\)
Hệ thức lượng tam giác vuông C'CD:
\(\dfrac{1}{CH^2}=\dfrac{1}{CD^2}+\dfrac{1}{C'C^2}\Rightarrow C'C=a\sqrt{6}\)