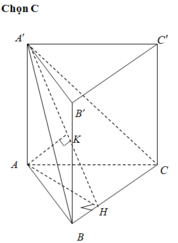
Gọi H là hình chiếu vuông góc của A lên BC.
Gọi K là hình chiếu vuông góc của A lên A’H.
Áp dụng định lí pytago vào tam giác vuông ABC ta tính được AB= a.
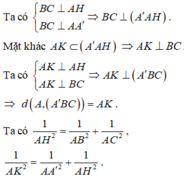
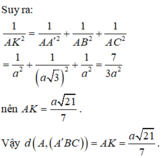

Gọi H là hình chiếu vuông góc của A lên BC.
Gọi K là hình chiếu vuông góc của A lên A’H.
Áp dụng định lí pytago vào tam giác vuông ABC ta tính được AB= a.
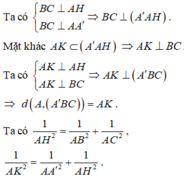
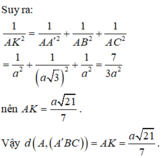
Cho hình lăng trụ đứng tam giác ABC. A’B’C’, có cạnh bên AA’ = 21 cm, tam giác ABC vuông cân tại A, BC = 42 cm. Tính khoảng cách từ A đến mặt phẳng (A’BC).
A. 21 2 c m
B. 21 2 2 c m
C. 21 2 c m
D. 21 2 4 c m
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, AB=a, AA’=2a. Tính khoảng cách từ điểm A đến mặt phẳng (A’BC).
A. 2 5 a
B. 2 5 a 5
C. 5 a 5
D. 3 5 a 5
Cho hình lăng trụ đứng ABC.A'B'C'. Cạnh bên AA' = a, ABC là tam giác vuông tại A có BC = 2a, AB = a 3 . Tính khoảng cách từ đỉnh A đến mặt phẳng (A'BC)
A . a 21 7
B . a 21 21
C . a 3 7
D . a 7 21
Cho lăng trụ đứng ABC. A’B’C’ có đáy ABC là tam giác vuông tại B, AB = a, AA’= 2a. Tính khoảng cách từ điểm A đến mặt phẳng (A’BC)
A. 2 5 a
B. 2 5 a 5
C. 5 a 5
D. 3 5 a 5
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B, AB=a, AA' = 2a Tính khoảng cách từ điểm A đến mặt phẳng (A'BC)
A. 2 5 a
B. 2 5 a 5
C. 5 a 5
D. 3 5 a 5
Cho hình lăng trụ đứng ABC. A'B'C' có đáy là tam giác ABC vuông tại A có BC=2a, A B = a 3 . Khoảng cách từ AA' đến mặt phẳng (BCC'B') là:
A. a 21 7
B. a 3 2
C. a 5 2
D. a 7 3
Cho lăng trụ ABC.A’B’C’ có cạnh bên bằng 2a, đáy ABC là tam giác vuông tại A, AB = a, AC = \(a\sqrt{3}\). Hình chiếu vuông góc của A’ lên (ABC) trùng với trung điểm I của BC. Khoảng cách giữa BB’ và AC’ bằng
Cho lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a, hình chiếu của A’ trên (ABC) trùng với tâm O của tam giác ABC. Biết A'O = a. Tính khoảng cách từ B’ đến mặt phẳng (A'BC)
A . 3 a 21
B . 3 a 4
C . 3 a 13
D . 3 a 28
Cho khối lăng trụ ABC.A’B’C’ có đáy là tam giác đều cạnh a và điểm A’ cách đều ba điểm A, B, C. Cạnh bên AA’ tạo với mặt phẳng đáy một góc 60 0 . Tính thể tích khối lăng trụ ABC.A’B’C’
A . a 3 3 10
B . a 3 3 12
C . a 3 3 4
D . a 3 3 8