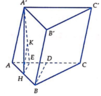
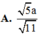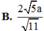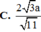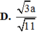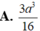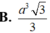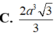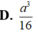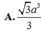Cho hình lăng trụ ABC.A'B'C' có mặt đáy ABC là tam giác đều, độ dài cạnh AB = 2a. Hình chiếu vuông góc của A' lên (ABC) trùng với trung điểm H của cạnh AB. Biết góc giữa cạnh bên và mặt đáy bằng 60 0 , tính theo a khoảng cách h từ điểm B đến mặt phẳng (ACC'A')
A . h = 39 a 13
B . h = 2 15 a 5
C . h = 2 21 a 7
D . h = 15 a 5
Đáp án B.
Do H là trung điểm AB nên
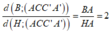
=> d(B;(ACC'A'))= 2d(H;(ACC'A'))
Ta có A'H ⊥ (ABC) nên
![]()
Gọi D là trung điểm của AC thì BD ⊥ AC
Kẻ HE
⊥
AC, ![]()
Ta có 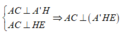
![]()
Trong (A'HE) kẻ HK
⊥
A'E, ![]()
Suy ra ![]()
![]() = 2HK
= 2HK
Ta có ![]()
![]()
Xét tam giác vuông A'AH có ![]()
Xét tam giác vuông A'HE có
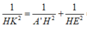
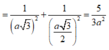
![]()
![]()