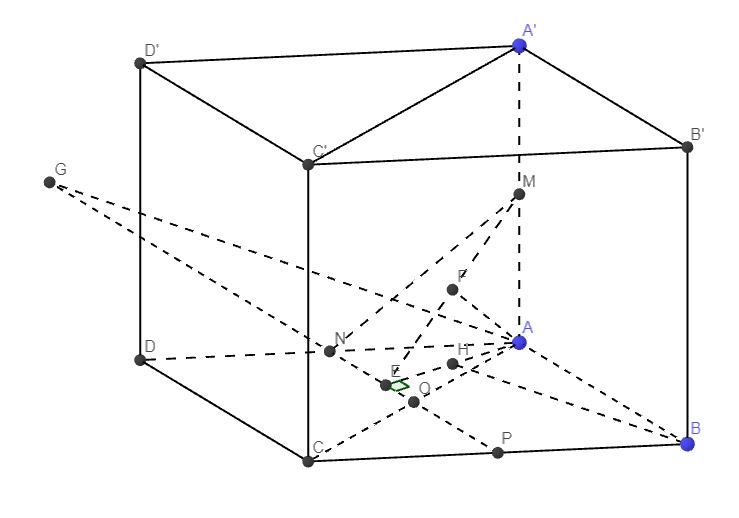
Gọi O là tâm đáy. Kẻ AE vuông góc NP, kẻ \(AF\perp ME\Rightarrow AF\perp\left(MNP\right)\)
ABPN là hình bình hành \(\Rightarrow\widehat{ANP}=180^0-\widehat{BAD}=60^0\)
\(\Rightarrow AE=AN.sin60^0=\sqrt{3}=AM\); \(NE=AN.cos60^0=1\); \(OE=ON-NE=\dfrac{1}{2}\)
\(\Rightarrow\Delta MAE\) vuông cân tại A \(\Rightarrow F\) đồng thời là trung điểm ME và \(AF=\dfrac{AM}{\sqrt{2}}=\dfrac{\sqrt{6}}{2}\)
Gọi H là trung điểm AE \(\Rightarrow FH=\dfrac{1}{2}AM=\dfrac{a\sqrt{3}}{2}\) và \(FH||AM\) (đường trung bình)
\(\Rightarrow FH\perp\left(ABCD\right)\Rightarrow FH\perp BH\) (1)
Trong mp (ABCD), qua A kẻ đường thẳng vuông góc AC cắt NP kéo dài tại G
\(\Rightarrow GA\perp\left(A'AC\right)\Rightarrow\widehat{FAG}\) hoặc góc bù với nó là góc giữa (MNP) và (A'AC)
\(OA=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2-2AD,CD.cos60^0}=\dfrac{\sqrt{13}}{2}\)
Hai tam giác vuông AEO và GAO đồng dạng (chung góc O)
\(\Rightarrow\dfrac{AG}{AE}=\dfrac{OA}{OE}\Rightarrow AG=\dfrac{AE.OA}{OE}=\sqrt{39}\)
\(GE=\sqrt{AG^2-AE^2}=6\Rightarrow GH=\sqrt{GE^2+\left(\dfrac{AE}{2}\right)^2}=\dfrac{7\sqrt{3}}{2}\)
\(\Rightarrow GF=\sqrt{GH^2+FH^2}=\sqrt{GH^2+\left(\dfrac{AM}{2}\right)^2}=\dfrac{5\sqrt{6}}{2}\)
\(cos\widehat{FAG}=\dfrac{AF^2+AG^2-GF^2}{2AF.AG}=\dfrac{\sqrt{26}}{26}\)
\(\Rightarrow sin\widehat{FAG}=\sqrt{1-\dfrac{1}{26}}=\dfrac{5}{\sqrt{26}}\)