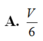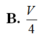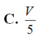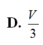Các câu hỏi tương tự
Cho hình hộp chữ nhật ABCD.ABCD có AD
2
a
. Tính theo a thể tích V của khối hộp ABCD.ABCD
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD= 2 a . Tính theo a thể tích V của khối hộp ABCD.A'B'C'D'
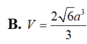
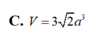
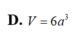
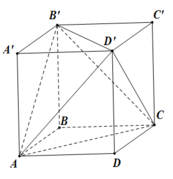
Cho hình hộp ABCD.A’B’C’D’. Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’
A. 7 3
B. 3
C. 8 3
D. 2
Cho hình hộp chữ nhật ABCD.ABCD có AD a; AB 2a. Diện tích mặt cầu ngoại tiếp tứ diện ACB’D’ là: A. 5π
a
2
B. 3π
a
2
C. 5π
a
2
/4 D. 5π
a
2
/3
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AD = a; AB' = 2a. Diện tích mặt cầu ngoại tiếp tứ diện ACB’D’ là:
A. 5π a 2
B. 3π a 2
C. 5π a 2 /4
D. 5π a 2 /3
Cho hình hộp chữ nhật ABCD.ABCD có AB a, AA - 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
π
2
a
3
. Tính thể tích V của hình chữ nhật A.
2
a
3
3
B.
2
a
3
C.
4...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA - 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π 2 a 3 .
Tính thể tích V của hình chữ nhật
A. 2 a 3 3
B. 2 a 3
C. 4 a 3
D. 4 a 3 3
Cho khối hộp chữ nhật ABCD.ABCD có thể tích là V. Biết AM MA, DN 3ND, CP 2PC. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Tính thể tích khối đa diện nhỏ hơn tính theo V bằng? A.
5
V
12
B.
7
V
12
C.
V
4
D.
V
6
Đọc tiếp
Cho khối hộp chữ nhật ABCD.A'B'C'D' có thể tích là V. Biết A'M = MA, DN = 3ND', CP = 2PC'. Mặt phẳng (MNP) chia khối hộp đã cho thành hai khối đa diện. Tính thể tích khối đa diện nhỏ hơn tính theo V bằng?
A. 5 V 12
B. 7 V 12
C. V 4
D. V 6
Cho hình hộp chữ nhật ABCD.ABCD có thể tích V
a
3
. Gọi M, N, P là trung điểm BC, CD, AA. Tính thể tích
V
1
của AMNP theo a. A. V
1
12
a
3
B. V
1
6
a
3
C. V
1
8
a
3
D...
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có thể tích V = a 3 . Gọi M, N, P là trung điểm BC, CD, AA'. Tính thể tích V 1 của AMNP theo a.
A. V = 1 12 a 3
B. V = 1 6 a 3
C. V = 1 8 a 3
D. V = 1 16 a 3
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.ABCD biết Thể tích V của khối hộp ABCD.ABCD là: A. V8. B. V
3
2
. C. V2. D. V4.
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp ABCD.A'B'C'D' biết Thể tích V của khối hộp ABCD.A'B'C'D' là:
A. V=8.
B. V= 3 2 .
C. V=2.
D. V=4.
Cho hình hộp chữ nhật
A
B
C
D
.
A
B
C
D
có
A
B
a
,
A
D
2
a
,
A
C
2
3
a
. Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’. A.
V
2
6
a
3
B...
Đọc tiếp
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' có A B = a , A D = 2 a , A C ' = 2 3 a . Tính theo a thể tích V của khối hộp ABCD.A’B’C’D’.
A. V = 2 6 a 3
B. V = 2 6 3 a 3
C. V = 3 2 a 3
D. V = 6 a 3
Cho hình hộp ABCD.A'B'C'D' có thể tích bằng V. Chọn trong các tứ diện sau, tứ diện nào có thê tích bằng V 3
A. A’BCD
B. A’BC’D
C. A’B’C’D
D. ABC’D