Các câu hỏi tương tự
Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số giữa thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi M và N theo thứ tự là trung điểm của A’B’ và B’C’. Tính tỉ số giữa thể tích khối chóp D’.DMN và thể tích khối hộp chữ nhật ABCD.A’B’C’D’
Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = a, BC = b, AA’ = c. Gọi E và F lần lượt là những điểm thuộc cạnh BB’ và DD’ sao cho BE = EB′/2, DF = FD′/2. Mặt phẳng (AEF) chia khối hộp chữ nhật ABCD.A’B’C’D’ thành hai khối đa diện (H) và (H’). Gọi (H’) là khối đa diện chứa đỉnh A’. Hãy tính thể tích của (H) và tỉ số thể tích của (H) và (H’).
Cho hình hộp ABCD.A'B'C'D' Tính tỉ số thể tích của khối tứ diện BDA'C' và khối hộp ABCD.A'B'C'D'
A. 1 5
B. 2 3
C. 1 3
D. 2 5
Cho khối hộp ABCD.A’B’C’D’. Gọi E và F theo thứ tự là trung điểm của các cạnh BB’ và DD’. Mặt phẳng (CEF) chia khối hộp trên làm hai khối đa diện. Tính tỉ số thể tích của hai khối đa diện đó.
Khối hộp ABCD.ABCD. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACBD. A.
7
3
B.
3
C.
8
3
D.
2
Đọc tiếp
Khối hộp ABCD.A'B'C'D'. Tính tỉ số thể tích của khối hộp đó và khối tứ diện ACB'D'.
A. 7 3
B. 3
C. 8 3
D. 2
Cho hình hộp ABCD.A’B’C’D’ có thể tích bằng 12
c
m
3
. Tính thể tích khối tứ diện AB’CD’. A. 2
c
m
3
. B. 3
c
m
3
. C. 4
c
m
3
. D. 5
c
m
3
.
Đọc tiếp
Cho hình hộp ABCD.A’B’C’D’ có thể tích bằng 12 c m 3 . Tính thể tích khối tứ diện AB’CD’.
A. 2 c m 3 .
B. 3 c m 3 .
C. 4 c m 3 .
D. 5 c m 3 .
Cho khối hộp ABCD.A'B'C'D'. Tính tỉ số thể tích của khối tứ diện ABDA' và khối hộp ABCD.A'B'C'D'
A. 1 3
B. 1 6
C. 1 2
D. 6
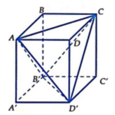
Cho hình hộp đứng ABCD.A’B’C’D’ có cạnh bên AAh và diện tích của tam giác ABC bằng S. Thể tích của khối hộp ABCD.A’B’C’D’ bằng
Đọc tiếp
Cho hình hộp đứng ABCD.A’B’C’D’ có cạnh bên AA'=h và diện tích của tam giác ABC bằng S. Thể tích của khối hộp ABCD.A’B’C’D’ bằng
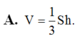
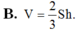
![]()
![]()