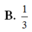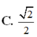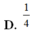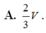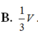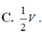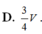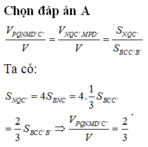Các câu hỏi tương tự
Cho khối lăng trụ ABC.A′B′C′ có thể tích bằng 1. Gọi M,N lần lượt là trung điểm của các đoạn thẳng AA′ và BB′. Đường thẳng CM cắt đường thẳng C′A′ tại P, đường thẳng CN cắt đường thẳng C′B′ tại Q. Thể tích của khối đa diện lồi A′MPB′NQ bằngCho mình hỏi sao suy ra được A′C′A′P,C′B′B′Q vậy ạ
Đọc tiếp
Cho khối lăng trụ ABC.A′B′C′ có thể tích bằng 1. Gọi M,N lần lượt là trung điểm của các đoạn thẳng AA′ và BB′. Đường thẳng CM cắt đường thẳng C′A′ tại P, đường thẳng CN cắt đường thẳng C′B′ tại Q. Thể tích của khối đa diện lồi A′MPB′NQ bằng
Cho mình hỏi sao suy ra được A′C′=A′P,C′B′=B′Q vậy ạ

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm trên cạnh SC sao cho EC 2ES. Gọi
α
là mặt phẳng chứa đường thẳng AE và song song với đường thẳng BD,
α
cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp S.AMEN. A.
V
6
B.
V
27
C.
V
9...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm trên cạnh SC sao cho EC = 2ES. Gọi α là mặt phẳng chứa đường thẳng AE và song song với đường thẳng BD, α cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp S.AMEN.
A. V 6
B. V 27
C. V 9
D. V 12
Cho hình hộp ABCD.ABCD, AB6cm, BCBB2cm. Điểm E là trung điểm cạnh BC. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng C E′, hai đỉnh P, Q nằm trên đường thẳng đi qua điểm B′ và cắt đường thẳng AD tại điểm F. Khoảng cách DF bằng A. 1cm B. 2cm C. 3cm D. 6cm
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D', AB=6cm, BC=BB'=2cm. Điểm E là trung điểm cạnh BC. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng C E′, hai đỉnh P, Q nằm trên đường thẳng đi qua điểm B′ và cắt đường thẳng AD tại điểm F. Khoảng cách DF bằng
A. 1cm
B. 2cm
C. 3cm
D. 6cm
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN2ND. Đường thẳng qua N vuông góc với BN cắt BC tại K. Tính thể tích V của khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là
Đọc tiếp
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN=2ND. Đường thẳng qua N vuông góc với BN cắt BC tại K. Tính thể tích V của khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK là

![]()
![]()
![]()

Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN2DN. Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK bằng
Đọc tiếp
Cho hình vuông ABCD cạnh a. Gọi N là điểm thuộc cạnh AD sao cho AN=2DN. Đường thẳng qua N vuông góc với BN cắt BC tại K. Thể tích khối tròn xoay tạo thành khi quay tứ giác ANKB quanh trục BK bằng
![]()
![]()
![]()
![]()
Cho hình hộp
A
B
C
D
.
A
B
C
D
có
B
A
D
^
B
A
A
^
D
A...
Đọc tiếp
Cho hình hộp A B C D . A ' B ' C ' D ' có B A D ^ = B A A ' ^ = D A A ' ^ = 60 0 , A B = A D = A A ' = a . Đường thẳng AC’ cắt các mặt phẳng ( A ' B D ) và ( C B ' D ' ) lần lượt tại M và N. Độ dài đoạn thẳng MN bằng
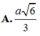
![]()
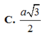
![]()
Cho hình lập phương ABCD.ABCD cạnh a. Gọi M, N lần lượt là trung điểm của AC và BC (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
Đọc tiếp
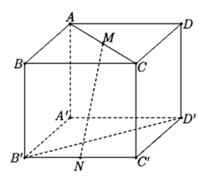
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C' (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
![]()
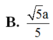
![]()
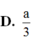
Cho hàm số
y
x
3
-
3
x
+
2
có đồ thị (C). Gọi (d) là đường thẳng đi qua A (3;20) và có hệ số góc m. Giá trị của m để đường thẳng (d) cắt (C) tại 3 điểm phân biệt:
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 có đồ thị (C). Gọi (d) là đường thẳng đi qua A (3;20) và có hệ số góc m. Giá trị của m để đường thẳng (d) cắt (C) tại 3 điểm phân biệt:
![]()
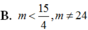
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và
S
A
⊥
A
B
C
D
. Trên đường thẳng vuông góc với tại D lấy điểm S’ thỏa mãn
S
D
1
2
S
A
và S, S’ ở cùng phía đối với mặt phẳng (ABCD). Gọi
V
1
là thể tích phần chung của hai khối chóp S.ABCD...
Đọc tiếp
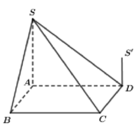
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và S A ⊥ A B C D . Trên đường thẳng vuông góc với tại D lấy điểm S’ thỏa mãn S ' D = 1 2 S A và S, S’ ở cùng phía đối với mặt phẳng (ABCD). Gọi V 1 là thể tích phần chung của hai khối chóp S.ABCD và S’.ABCD. Gọi V 2 là thể tích khối chóp S.ABCD, tỉ số V 1 V 2 bằng
![]()