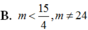Các câu hỏi tương tự
Cho hàm số
y
-
x
+
1
2
x
-
1
có đồ thị là (C) , đường thẳng d: yx+m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B. Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A; B . Tìm m để tổng k1+k2 đạt giá trị lớn nhất. A. m-1. B.m-2 . C. m3 . D. m-5.
Đọc tiếp
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y=x+m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B. Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A; B . Tìm m để tổng k1+k2 đạt giá trị lớn nhất.
A. m=-1.
B.m=-2 .
C. m=3 .
D. m=-5.
Cho hàm số
y
-
x
+
1
2
x
-
1
có đồ thị là (C) , đường thẳng d: y x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất. A. -2 B. -1 C. 1 D. 2
Đọc tiếp
Cho hàm số y = - x + 1 2 x - 1 có đồ thị là (C) , đường thẳng d: y= x+ m. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A: B . Gọi k1; k2 lần lượt là hệ số góc của các tiếp tuyến với ( C) tại A; B . Tìm m để tổng k1+ k2 đạt giá trị lớn nhất.
A. -2
B. -1
C. 1
D. 2
Cho hàm số
y
x
3
-
3
x
2
+
4
có đồ thị (C) , đường thẳng (d): ym(x+1) với m là tham số, đường thẳng
∆
:
y
2
x
-
7
. Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với
∆
và...
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C) , đường thẳng (d): y=m(x+1) với m là tham số, đường thẳng ∆ : y = 2 x - 7 . Tìm tổng tất cả các giá trị của tham số m để đường thẳng (d) cắt đồ thị (C) tại 3 điểm phân biệt A(-1;0); B;C sao cho B,C cùng phía với ∆ và d B ; ∆ + d C ; ∆ = 6 5 .
A. 0
B. 8
C. 5
D. 4
Cho hàm số: y x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng
2
7
là A. m-1 B. m-1 hoặc m4 C. m4 D. Không tồn tại m
Đọc tiếp
Cho hàm số: y = x3+2mx2+3(m-1)x+2 có đồ thị (C) . Đường thẳng d: y= - x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0; -2); B và C. Với M(3;1) giá trị của tham số m để tam giác MBC có diện tích bằng 2 7 là
A. m=-1
B. m=-1 hoặc m=4
C. m=4
D. Không tồn tại m
Cho hàm số yx3-3x2+4 có đồ thị (C) . Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là A. 4 B. 1 C. 6 D. vô số
Đọc tiếp
Cho hàm số y=x3-3x2+4 có đồ thị (C) . Gọi d là đường thẳng qua I(1; 2) với hệ số góc k . Có bao nhiêu giá trị nguyên của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. 4
B. 1
C. 6
D. vô số
Cho hàm số
y
x
3
-
3
x
2
+
4
có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là A. {0} B. R C. {-3} D. (-3; +∞).
Đọc tiếp
Cho hàm số y = x 3 - 3 x 2 + 4 có đồ thị (C). Gọi d là đường thẳng qua I(1; 2) với hệ số góc k. Tập tất cả các giá trị của k để d cắt (C) tại ba điểm phân biệt I, A, B sao cho I là trung điểm của đoạn thẳng AB là
A. {0}
B. R
C. {-3}
D. (-3; +∞).
Cho hàm số y
2
x
+
1
x
+
1
có đồ thị (C) và đường thẳng d: y x + m. Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho AB
10
là: A. m -1 hoặc m 6 B. 0
≤
m
≤
5 C. m 0 hoặc m 6 D. m 0 hoặc m 7
Đọc tiếp
Cho hàm số y = 2 x + 1 x + 1 có đồ thị (C) và đường thẳng d: y = x + m. Giá trị của tham số m để d cắt (C) tại hai điểm phân biệt A, B sao cho AB = 10 là:
A. m = -1 hoặc m = 6
B. 0 ≤ m ≤ 5
C. m = 0 hoặc m = 6
D. m = 0 hoặc m = 7
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k . Tìm k để đường thẳng d cắt đồ thị hàm số C: y x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1? A. k 2 B. k -1 C. k 1 D. Đáp án khác
Đọc tiếp
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k . Tìm k để đường thẳng d cắt đồ thị hàm số C: y= x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1?
A. k =2
B. k= -1
C. k= 1
D. Đáp án khác
Cho (C) là đồ thị của hàm số y(x-2)/(x+1) và đường thẳng d:ymx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C) A. B. C. D.
Đọc tiếp
Cho (C) là đồ thị của hàm số y=(x-2)/(x+1) và đường thẳng d:y=mx+1. Tìm các giá trị thực của tham số m để đường thẳng d cắt đồ thị hàm số (C) tại hai điểm A,B phân biệt thuộc hai nhánh khác nhau của (C)
A.![]()
B.![]()
C.![]()
D. ![]()