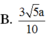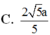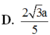Chọn B
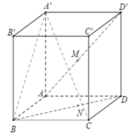
* Sử dụng định lí Ta-lét đảo.
Ta có: ![]()
![]()
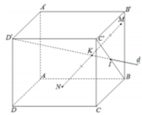
Áp dụng định lí Ta-lét đảo, ta có AD, MN, BD' lần lượt nằm trên ba mặt phẳng song song.
=> M song song với mặt phẳng (P) chứa BD' và song song với AD.
Nên MN//(BCD'A') hay MN//(A'BC)
* Sử dụng định lí Ta-lét.
* Sử dụng định lí Ta-lét.
Vì AD//A'D' nên tồn tại (P) là mặt phẳng qua AD và song song với mp (A'D'CB)
(Q) là mặt phẳng qua M và song song với mp (A'D'CB). Giả sử (Q) cắt DB tại N
Theo định lí Ta-lét ta có: ![]()
Mà các mặt của hình hộp là hình vuông cạnh a nên AD' = DB = a 2
Từ (*), ta có: AM = DN' => DN' = DN
![]()
(Q)//(A'D'CB) suy ra luôn song song với mặt phẳng cố định (A'D'CB) hay (A'BC)