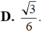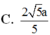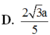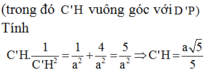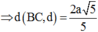Các câu hỏi tương tự
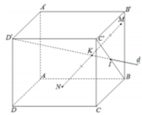
Cho hình lập phương ABCD.ABCD cạnh a. Gọi M, N lần lượt là trung điểm của AC và BC (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C' (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
![]()
![]()
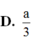
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
y
-
5
2
z
-...
Đọc tiếp
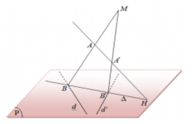
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x - 2 1 = y - 5 2 = z - 2 1 , d ' : x - 2 1 = y - 1 - 2 = z - 2 1 và hai điểm A(a;0;0), B(0;0;b). Gọi (P) là mặt phẳng chứa d và d'; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng D thay đổi trên (P) nhưng luôn đi qua H đồng thời D cắt d và d' lần lượt tại B, B'. Hai đường thẳng cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có véc tơ chỉ phương u → = ( 15 ; - 10 ; - 1 ) (tham khảo hình vẽ). Tính T= a+b
A. T = 8
B. T = 9
C. T = -9
D. 6
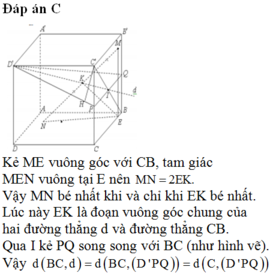
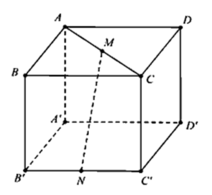
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
![]()
Cho hình lập phương ABCD.ABCD cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng
A
A
,
B
B
,
C
C
thỏa mãn diện tích của tam giác MNP bằng
a
2
. Góc giữa hai mặt phẳng (MNP) và (ABCD) là
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng A A ' , B B ' , C C ' thỏa mãn diện tích của tam giác MNP bằng a 2 . Góc giữa hai mặt phẳng (MNP) và (ABCD) là
![]()
![]()
![]()
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi M, N lần lượt là trung điểm của cạnh AA' và A'B'. Số đo góc giữa hai đường thẳng MN và BD (như hình vẽ bên) là:
A. 45°.
B. 30°.
C. 60°.
D. 90°.
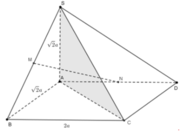
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC, biết MN
a
6
2
. Khi đó giá trị sin của góc giữa đường thẳng MN và mặt phẳng (SBD) bằng A.
2
5
. B.
3...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, tâm O. Gọi M và N lần lượt là trung điểm của hai cạnh SA và BC, biết MN = a 6 2 . Khi đó giá trị sin của góc giữa đường thẳng MN và mặt phẳng (SBD) bằng
A. 2 5 .
B. 3 3 .
C. 5 5 .
D. 3 .
Cho hình chóp tứ giác đều
S
.
A
B
C
D
có cạnh đáy bằng a tâm O. Gọi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thẳng MN và mặt phẳng
A
B
C
D
bằng
60
0
. Tính cosin góc giữa đường thẳng và mặt phẳng
(
S
B
D
)
.
Đọc tiếp
Cho hình chóp tứ giác đều S . A B C D có cạnh đáy bằng a tâm O. Gọi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thẳng MN và mặt phẳng A B C D bằng 60 0 . Tính cosin góc giữa đường thẳng và mặt phẳng ( S B D ) .
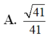
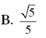
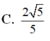
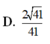
Cho hình chóp S.ABCD có đáy là hình thang.
A
D
/
/
B
C
,
A
D
2
B
C
2
a
. Gọi E, F lần lượt là trọng tâm các tam giác SAD và SBC. Gọi d là giao tuyến của hai mặt phẳng (EBC) và (FAD); M,N lần lượt là giao điểm của d với các mặt phẳng (SAB), (SCD). Độ dài đoạn thẳng MN bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thang. A D / / B C , A D = 2 B C = 2 a . Gọi E, F lần lượt là trọng tâm các tam giác SAD và SBC. Gọi d là giao tuyến của hai mặt phẳng (EBC) và (FAD); M,N lần lượt là giao điểm của d với các mặt phẳng (SAB), (SCD). Độ dài đoạn thẳng MN bằng
![]()
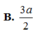
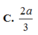
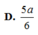
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB
2
a
, AD2a, SA vuông góc với đáy và SA
2
a
Gọi M và N lần lượt là trung điểm của SB và AD( tham khảo hình vẽ). Côsin góc giữa đường thẳng MN và mặt phẳng (SAC) bằng
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB= 2 a , AD=2a, SA vuông góc với đáy và SA= 2 a Gọi M và N lần lượt là trung điểm của SB và AD( tham khảo hình vẽ). Côsin góc giữa đường thẳng MN và mặt phẳng (SAC) bằng