Chọn đáp án C.
Gọi P là trung điểm cạnh A'D' khi đó BD//NP.
Khi đó góc giữa ![]()
Vì ABCD.A'B'C'D' là hình lập phương cạnh a nên ![]()
Suy ra 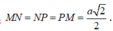
Do đó tam giác MNP đều ![]()
Chọn đáp án C.

Gọi P là trung điểm cạnh A'D' khi đó BD//NP.
Khi đó góc giữa ![]()
Vì ABCD.A'B'C'D' là hình lập phương cạnh a nên ![]()
Suy ra 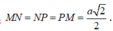
Do đó tam giác MNP đều ![]()
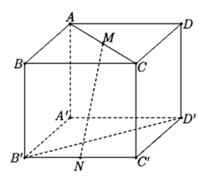
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M, N lần lượt là trung điểm của AC và B'C' (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
![]()
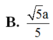
![]()
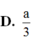
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Gọi M, N lần lượt là trung điểm của BC và DD'. Tính theo a khoảng cách giữa hai đường thẳng MN và BD.
A. 3 a
B. 3 a 2
C. 3 a 3
D. 3 a 6
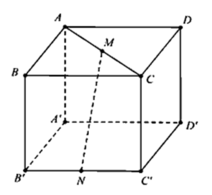
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Gọi M, N lần lượt là trung điểm của AC và B’C’ (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng MN và B’D’ bằng
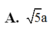
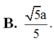
![]()
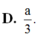
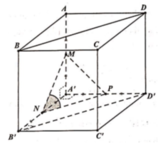
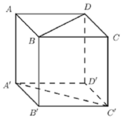
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Một đường thẳng d đi qua đỉnh D¢ và tâm I của mặt bên BCC'B'. Hai điểm M, N thay đổi lần lượt thuộc các mặt phẳng (BCC'B') và (ABCD) sao cho trung điểm K của MN thuộc đường thẳng d (tham khảo hình vẽ). Giá trị bé nhất của độ dài đoạn thẳng MN là
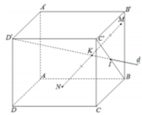
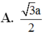
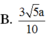
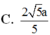
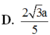
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Gọi E, F lần lượt là trung điểm của B'C' và AD. Gọi α là số đo của góc giữa hai mặt phẳng (BEF) và (ADD’A’). Khi đó cos α bằng
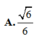
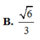
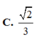
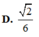
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Các điểm M, N, P lần lượt thuộc các đường thẳng A A ' , B B ' , C C ' thỏa mãn diện tích của tam giác MNP bằng a 2 . Góc giữa hai mặt phẳng (MNP) và (ABCD) là
![]()
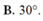
![]()
![]()
Cho hình chóp đều S.ABCD có tất cả các cạnh đều bằng a. Gọi M, N lần lượt là trung điểm của AD và SD. Số đo của góc giữa hai đường thẳng MN và SC.
![]()
![]()
![]()
![]()
Cho hình lập phương A B C D . A ' B ' C ' D ' có cạnh bằng a, gọi α là góc giữa đường thẳng A ' B và mặt phẳng B B ' D ' D . Tính sin α
A. 3 5
B. 3 2
C. 1 2
D. 3 4
Cho hình lập phương ABCD.A'B'C'D' có cạnh bên bằng a (tham khảo hình vẽ bên). Gọi α là góc giữa đường thẳng A'C và mặt phẳng (A'B'C'D') thì:
![]()

![]()
![]()