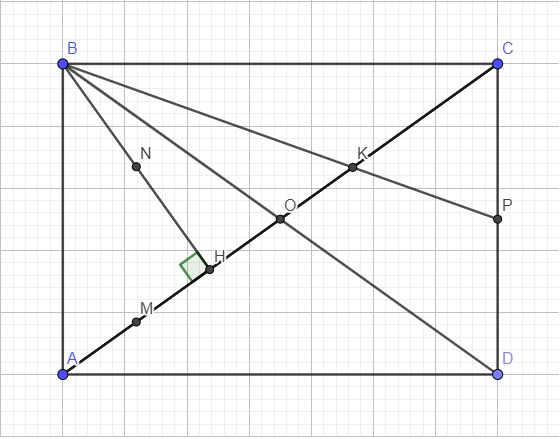
Gọi O là giao điểm AC và BD \(\Rightarrow\) O đồng thời là trung điểm AC và BD theo t/c hình chữ nhật
Trong tam giác BCD, ta có P là trung điểm CD và O là trung điểm BD
\(\Rightarrow K\) là trọng tâm tam giác BCD
\(\Rightarrow CK=\dfrac{2}{3}CO\)
Mà O là trung điểm AC \(\Rightarrow CO=\dfrac{1}{2}AC\)
\(\Rightarrow CK=\dfrac{2}{3}.\dfrac{1}{2}AC=\dfrac{1}{3}AC\)
\(\Rightarrow AC=3CK\)
Cho hình chữ nhật AB =2AD .Vẽ BH vuông góc với AC .Gọi M ,N ,P lần lượt là trung điểm của AH ,BH ,CD . a) tính diện tích của hình chữ nhật ABCD biết AB =8. Chứng minh tứ giác MNCP là hình bình hành. b) Chứng minh MP vuông góc MB
Cho hình chữ nhật ABCD. Vẽ BH vuông góc với AV. Gọi M,N,P lần lượt là trung điểm của AH,BH,CD
a) Chứng minh MNCP là hình bình hành
b) Chứng minh N là trực tâm tam giác MBC
c)Chứng minh MP vuông góc MB
d) gọi I là trung điểm BP và J là giao đỉm AC và NP. Chứng minh rằng 2(MI-Ị)<NP
Cho hình chữ nhật ABCD cóa AB=2AD. Vẽ BH vuông góc với AC. Gọi M,N,P lần lượt là trung điểm của AH, BH, CD
a, chứng minh MNCP là hbh
b, Chứng mình MP vuông góc MB
c, Gọi I là trung điểm của BP và J là giao điểm của MC và NP. Chứng minh MI- IJ < IP
Cho hình chữ nhật ABCD, kẻ BH vuông góc với AC. Gọi N là trung điểm của BH, M là trung điểm của AH. Biết AB = 4cm. Gọi K là trung điểm của CD.
a. Tính MN.
b. Chứng minh tứ giác MNCK là hình bình hành.
c. Chứng minh tam giác MBK vuông tại M.
d. Chứng minh 𝐵𝐾𝑀^= 𝐵𝐶𝑀^
Cho hình chữ nhật ABCD có AB<BC,kẻ BH vuông góc AC (H thuộc AC).Gọi M,K,N lần lượt là trung điểm của AH,CD và BH
a) Chứng minh MNCK là hình bình hành
b)Chứng minh BM vuông góc MK
Cho hình chữ nhật ABCD có AB = 8cm; BC = 6cm. Kẻ BH vuông góc với AC tại H, DM vuông góc với AC tại M.
a) Chứng minh ∆ABH đồng dạng với ∆ACB và suy ra AC.AH = AB^2.
b) Tính độ dài các đoạn thẳng AC, BH, CH.
c) Gọi I là điểm đối xứng với B qua AC. Chứng minh DM = IH và ACID là hình thang cân.
d) Gọi E, F lần lượt là trung điểm của AH, CD và K là giao điểm của BF với AC. Chứng minh rằng BF.EK ≥ BE.EF.
Cho hình chữ nhật ABCD có AB = 2AD. Vẽ BH vuông góc với AC . Gọi M,N,P lần lượt là trung điểm của AH,BH,CD. Gọi I là trung điểm của BP và J là giao điểm của MC và NP.
A.MI – IJ > IP
B. MI < IP + IJ
C.MI < IP-– IJ
D.MI + IJ < IP
KO CẦN GIẢI THÍCH
Cho hình chữ nhật ABCD, kẻ AH vuông góc với BD tại H.
a) Chứng minh tam giác ADH đồng dạng với tam giác BAH, suy ra AH2=DH.BH
b) Tính AD, AB biết DH = 9 cm, BH = 16 cm.
c) Gọi K,M,N lần lượt là trung điểm của AH, BH, CD. Chứng minh tứ giác MNDK là hình bình hành và góc AMN = 90°
Cho hình chữ nhật ABCD. Vẽ BH vuông góc AC tại H, gọi M là trung điểm BH và N là trung điểm AH.
a) Chứng minh MN song song AB và tứ giác ABMN là hình thang.
b) Gọi E là trung điểm CD. Chứng minh tứ giác MNEC là hình bình hành.
c) Tính số đo góc BNE.
Cho hình chữ nhật ABCD. Vẽ BH vuông góc AC tại H, gọi M là trung điểm BH và N là trung điểm AH.
a) Chứng minh MN song song AB và tứ giác ABMN là hình thang.
b) Gọi E là trung điểm CD. Chứng minh tứ giác MNEC là hình bình hành.
c) Tính số đo góc BNE.
