Các câu hỏi tương tự
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và SC. Mặt phẳng (BMN) cắt SD tại điểm P. Đặt
t
V
S
.
B
M
P
N
V
S
.
A
B
C...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và SC. Mặt phẳng (BMN) cắt SD tại điểm P. Đặt t = V S . B M P N V S . A B C D . Tìm t.
A. t = 1 8
B. t = 1 12
C. t = 1 6
D. t = 1 16
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, gọi M là trung điểm của cạnh bên SC. Mặt phẳng (P) qua AM và song song với BD lần lượt cắt các cạnh bên SB, SD tại N, Q. Đặt
t
V
S
.
A
N
M
Q
V
S
.
A
B...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, gọi M là trung điểm của cạnh bên SC. Mặt phẳng (P) qua AM và song song với BD lần lượt cắt các cạnh bên SB, SD tại N, Q. Đặt t = V S . A N M Q V S . A B C D . Tính t
A. 1 3
B. 2 5
C. 1 6
D. 1 4
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SA. Mặt phẳng (BCM) cắt cạnh SD tại điểm N. Đặt
t
V
S
.
B
C
N
M
V
S
.
A
B
C
D...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là trung điểm của cạnh SA. Mặt phẳng (BCM) cắt cạnh SD tại điểm N. Đặt t = V S . B C N M V S . A B C D . Tìm t.
A. 3 4
B. 1 4
C. 3 8
D. 1 8
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB. SC và P là điểm trên cạnh SD sao cho
S
P
S
D
3
4
. Mặt phẳng (MNP) cắt cạnh SB tại điểm Q. Tỉ số
S
Q
S
B
bằng A.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh AB. SC và P là điểm trên cạnh SD sao cho S P S D = 3 4 . Mặt phẳng (MNP) cắt cạnh SB tại điểm Q. Tỉ số S Q S B bằng
A. 3 4
B. 2 3
C. 2 5
D. 4 3
Cho hình chóp S.ABCD có đáy hình thoi cạnh 3a, SASD3a, SBSC3a
3
.
Gọi M, N lần lượt là trung điểm của các cạnh SA và SD, P là điểm thuộc cạnh AB sao cho AP2a Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP)
Đọc tiếp
Cho hình chóp S.ABCD có đáy hình thoi cạnh 3a, SA=SD=3a, SB=SC=3a 3 . Gọi M, N lần lượt là trung điểm của các cạnh SA và SD, P là điểm thuộc cạnh AB sao cho AP=2a Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP)
![]()
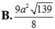
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a, SA SD 3a, SB SC
3
a
3
. Gọi M, N lần lượt là trung điểm của cạnh SA và SD, P là điểm thuộc cạnh AB sao cho AP 2a. Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP). A.
9
a
2
139
4
B. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình thoi cạnh 3a, SA = SD = 3a, SB = SC = 3 a 3 . Gọi M, N lần lượt là trung điểm của cạnh SA và SD, P là điểm thuộc cạnh AB sao cho AP = 2a. Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP).
A. 9 a 2 139 4
B. 9 a 2 139 8
C. 9 a 2 7 8
D. 9 a 2 139 16
Cho khối chóp S.ABCD có đáy là hình bình hành, thể tích bằng 1. Gọi M là trung điểm cạnh SA; các điểm E,F lần lượt là điểm đối xứng của A qua B và D. Mặt phẳng (MEF) cắt các cạnh SB,SD lần lượt tại các điểm N,P. Thể tích của khối đa diện ABCDMNP bằng A.
2
3
B.
1
3
C.
3
4
D.
1
4
Đọc tiếp
Cho khối chóp S.ABCD có đáy là hình bình hành, thể tích bằng 1. Gọi M là trung điểm cạnh SA; các điểm E,F lần lượt là điểm đối xứng của A qua B và D. Mặt phẳng (MEF) cắt các cạnh SB,SD lần lượt tại các điểm N,P. Thể tích của khối đa diện ABCDMNP bằng
A. 2 3
B. 1 3
C. 3 4
D. 1 4
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I là trung điểm cạnh SC. Xét (α) là mặt phẳng thay đổi qua AI và cắt các cạnh SB, SD lần lượt tại M và N. Tổng giá trị nhỏ nhất là lớn nhất của biểu thức
T
S
M
S
B
+
S
N
S
D
bằng A.
17
6...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi I là trung điểm cạnh SC. Xét (α) là mặt phẳng thay đổi qua AI và cắt các cạnh SB, SD lần lượt tại M và N. Tổng giá trị nhỏ nhất là lớn nhất của biểu thức T = S M S B + S N S D bằng
A. 17 6
B. 13 6
C. 7 3
D. 5 3
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là điểm di động trên cạnh SC (M không trùng S và C), mặt phẳng (α) chứa đường thẳng AM song song với BD lần lượt cắt các cạnh SB, SD tại E và F. Giá trị
T
S
B
S
E
+
S
D
S
F
-
S...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là điểm di động trên cạnh SC (M không trùng S và C), mặt phẳng (α) chứa đường thẳng AM song song với BD lần lượt cắt các cạnh SB, SD tại E và F. Giá trị T = S B S E + S D S F - S C S M bằng
A. 1
B. 2
C. 1 2
D. 3 2



