Chọn A
Gọi O là gia điểm của hai đường chéo của hình bình hành ABCD. Gọi I là giao điểm của SO và AM. Khi đó
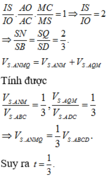
Chọn A
Gọi O là gia điểm của hai đường chéo của hình bình hành ABCD. Gọi I là giao điểm của SO và AM. Khi đó
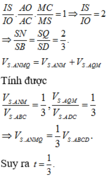
Cho hình chóp tứ giác đều S.ABCD, đáy là hình vuông cạnh a, cạnh bên tạo với góc 60 ° . Gọi M là trung điểm của SC. Mặt phẳng qua AM và song song với BD, cắt SB, SD lần lượt tại E và F và chia khối chóp thành hai phần. Tính thể tích V của khối chóp không chứa đỉnh S.
A. V = a 3 6 36
B. V = a 3 6 9
C. V = a 3 6 18
D. V = a 3 6 12
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên tạo với đáy một góc 60 o . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD cắt SB tại E và cắt SD tại F. Tính thể tích V khối chóp S.AEMF.
A. V = a 3 6 36 .
B. V = a 3 6 9 .
C. V = a 3 6 6 .
D. V = a 3 6 18 .
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M là điểm di động trên cạnh SC (M không trùng S và C), mặt phẳng (α) chứa đường thẳng AM song song với BD lần lượt cắt các cạnh SB, SD tại E và F. Giá trị T = S B S E + S D S F - S C S M bằng
A. 1
B. 2
C. 1 2
D. 3 2
Cho hình chóp S . A B C D có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5 S M = 2 S C , mặt phẳng α qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D
A. 1 5
B. 8 35
C. 1 7
D. 6 35
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm trên cạnh SC sao cho EC=2ES , α là mặt phẳng chứa đường thẳng AE và song song với đường thẳng BD, cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp S.AMEN.
A. V 6
B. V 27
C. V 9
D. V 12
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích V. Gọi E là điểm trên cạnh SC sao cho EC = 2ES. Gọi α là mặt phẳng chứa đường thẳng AE và song song với đường thẳng BD, α cắt hai cạnh SB, SD lần lượt tại hai điểm M, N. Tính theo V thể tích khối chóp S.AMEN.
A. V 6 .
B. V 27 .
C. V 9 .
D. V 12 .
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M là điểm trên cạnh SC sao cho 5 S M = 2 S C , mặt phẳng α đi qua A, M và song song với đường thẳng BD cắt hai cạnh SB, SD lần lượt tại hai điểm H, K. Tính tỉ số thể tích V S . A H M K V S . A B C D .
A. 1 5
B. 8 35
C. 1 7
D. 6 35
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x (0<x<a). Mặt phẳng ( α ) qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5
Cho hình chóp S.ABCD với đáy ABCD là hình vuông cạnh a, cạnh bên SB = b và tam giác SAC cân tại S. Trên cạnh AB lấy điểm M với AM = x 0 < x < α . Mặt phẳng α qua M song song với AC, SB và cắt BC, SC, SA lần lượt tại N, P, Q. Xác định x để diện tích thiết diện MNPQ đạt giá trị lớn nhất.
A. x = a 4
B. x = a 3
C. x = a 2
D. x = a 5