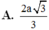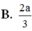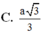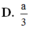Đáp án là C

Ta có:
![]()
theo giao tuyến SD.
Trong (SAD) kẻ AH ⊥ DS
![]()
![]()
![]()
Ta có
![]()
Theo bài
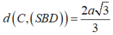

Vì tứ diện SABD có ba cạnh AS, AB, AD đôi một vuông góc nên



Do đó tam giác SAD vuông cân tại A có:
![]()

Đáp án là C

Ta có:
![]()
theo giao tuyến SD.
Trong (SAD) kẻ AH ⊥ DS
![]()
![]()
![]()
Ta có
![]()
Theo bài
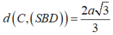

Vì tứ diện SABD có ba cạnh AS, AB, AD đôi một vuông góc nên



Do đó tam giác SAD vuông cân tại A có:
![]()

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; S A ⊥ A B C D và SA=2a. Tính khoảng cách d từ điểm B đến mặt phẳng (SCD)
A. d = a 5 5 .
B. d = a
C. d = 4 a 5 5 .
D. d = 2 a 5 5 .
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD = 2a, AB = BC = SA = a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).
A. h = a 3
B. h = a 6 6
C. h = a 6 3
D. h = a 3 6
Cho hình chóp S.ABCD có đáy là nửa lục giác đều ABCD nội tiếp trong đường kính AD=2a và có cạnh SA ⊥ (ABCD), SA=a 6 . Tính khoảng cách từ B đến mặt phẳng (SCD).
A. a 2
B. a 3
C. a 2 2
D. a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A D = 2 a ; S A ⊥ A B C D và SA = a. Khoảng cách từ A đến mặt phẳng (SCD) bằng
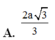
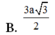
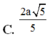
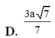
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA ⊥ ( A B C D ) và SA=2a.Tính khoảng cách d từ điểm B đến mặt phẳng (SCD).
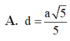
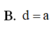
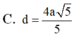
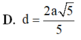
Cho hình chóp S.ABCD có đáy là hình thang với AB = 2a là đáy lớn, BC =
CD = DA = a, SA ⊥ (ABCD) và (SBD) tạo với đáy một góc 45◦. Tính khoảng cách từ C đến (SBD).
Cho hình chóp S.ABCD có SA ⊥ (ABCD),SA=2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
A. a 2 4
B. a 3 3
C. a 3 4
D. a 2 3
Hình chóp S.ABCD đáy hình vuông cạnh a; SA ⊥ (ABCD); SA=a 3 . Khoảng cách từ B đến mặt phẳng (SCD) bằng:
![]()
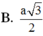
![]()
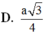
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB=a, AD=2a; SA vuông góc với đáy ABCD, SC hợp với đáy một góc α và tan α . Khi đó, khoảng cách từ điểm B đến mặt phẳng (SCD) là: