Đáp án B
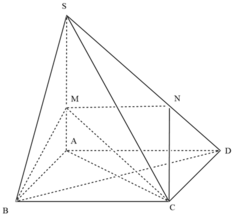
Kẻ MN // AD // AD nên (MBC) cắt (SAD) theo giao tuyến là MN


Đáp án B

Kẻ MN // AD // AD nên (MBC) cắt (SAD) theo giao tuyến là MN


Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O cạnh bằng a, A B C ^ = 60 0 , SA=SB=SC, SD= 2a. Gọi (P) là mặt phẳng qua A và vuông góc với SB tại K. Mặt phẳng (P) chia khối chóp S.ABCD thành hai phần có thể tích V 1 ; V 2 trong đó V 1 là thể tích khối đa diện chứa đỉnh S. Tính V 1 V 2
A. 11
B. 7
C. 9
D. 4
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD) và SA = a. Thể tích của khối chóp S.ABCD bằng
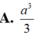
![]()
![]()

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy (ABCD). Biết thể tích khối chóp S.ABCD bằng a 3 3 6 . Độ dài cạnh bên SA bằng bao nhiêu?
![]()
![]()
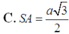
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng đáy, khối chóp S.ABCD có thể tích bằng a 3 2 3 . Gọi α là góc giữa hai mặt phẳng (SAD) và (SBD). Tính cos α.
A. cos α = 3 5
B. cos α = 6 3
C. cos α = 2 2 5
D. cos α = 10 5
Cho khối chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = b, SA vuông góc với đáy, SA = 2a. Điểm M thuộc đoạn SA, AM = x. Giá trị của x để mặt phẳng (MBC) chia khối S.ABCD thành hai khối có thể tích bằng nhau là:
A . x = ( 2 + 5 ) a
B . x = ( 3 + 5 ) a
C . x = ( 2 - 5 ) a
D . x = ( 3 - 5 ) a
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a , cạnh bên SA vuông góc với mặt phẳng đáy và S A = a 6 Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 6 6
B. V = a 3 6 4
C. V = a 3 6 3
D. V = a 3 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy và SA= a 2 Tính thể tích V của khối chóp S.ABCD
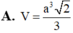
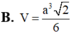
![]()
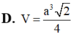
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và (ABCD) bằng 45 0 . Gọi M, N lần lượt là trung điểm của AB, AD. Tính thể tích khối chóp S.CDMN theo a
A . 5 a 3 8
B . a 3 8
C . 5 a 3 24
D . a 3 3
Khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA=3a và SA vuông góc với mặt đáy. Thể tích của khối chóp S.ABCD là
A. 6 a 3
B. a 3
C. a 3 3
D. 3 a 3