Các câu hỏi tương tự
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử (α) là mặt phẳng đi qua A và vuông góc với cạnh SC, (α) cắt SC tại I.a) Xác định giao điểm K của SO với mặt phẳng (α).b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // (α).c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng (α). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (α).
Đọc tiếp
Hình chóp S.ABCD có đáy là hình vuông ABCD tâm O và có cạnh SA vuông góc với mặt phẳng (ABCD). Giả sử (α) là mặt phẳng đi qua A và vuông góc với cạnh SC, (α) cắt SC tại I.
a) Xác định giao điểm K của SO với mặt phẳng (α).
b) Chứng minh mặt phẳng (SBD) vuông góc với mặt phẳng (SAC) và BD // (α).
c) Xác định giao tuyến d của mặt phẳng (SBD) và mặt phẳng (α). Tìm thiết diện cắt hình chóp S.ABCD bởi mặt phẳng (α).
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB 2a, AD DC a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA a.a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
Đọc tiếp
Hình chóp S.ABCD có đáy là hình thang vuông ABCD vuông tại A và D, có AB = 2a, AD = DC = a, có cạnh SA vuông góc với mặt phẳng (ABCD) và SA = a.
a) Chứng minh mặt phẳng (SAD) vuông góc với mặt phẳng (SDC), mặt phẳng (SAC) vuông góc với mặt phẳng (SCB).
b) Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABCD), tính tanφ.
c) Gọi (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC). Hãy xác định (α) và xác định thiết diện của hình chóp S.ABCD với (α)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và
S
A
a
6
(hình vẽ). Gọi α là góc giữa đường thẳng SB và mặt phẳng (SAC). Tính sin α ta được kết quả là A.
1
14
B.
2
2
C.
3
2
D.
1
5...
Đọc tiếp
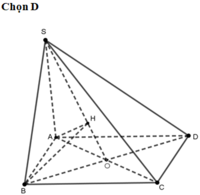
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. SA vuông góc với mặt phẳng (ABCD) và S A = a 6 (hình vẽ). Gọi α là góc giữa đường thẳng SB và mặt phẳng (SAC). Tính sin α ta được kết quả là
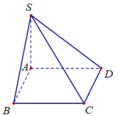
A. 1 14
B. 2 2
C. 3 2
D. 1 5
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với ABBCa ,AD2a Cạnh SA2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và
(
α
)
là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng
(
α
)
với hình chóp S.ABCD là
Đọc tiếp
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=a ,AD=2a Cạnh SA=2a và SA vuông góc với mặt phẳng (ABCD). Gọi M là trung điểm của cạnh AB và ( α ) là mặt phẳng qua M và vuông góc với AB. Diện tích thiết diện của mặt phẳng ( α ) với hình chóp S.ABCD là
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh, a góc giữa mặt bên và mặt phẳng đáy là α thoả mãn
cos
α
1
3
Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị nào trong các giá trị sau A. 0,11. B. 0,13. C. 0,7. D. 0,9.
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông ABCD cạnh, a góc giữa mặt bên và mặt phẳng đáy là α thoả mãn cos α = 1 3 Mặt phẳng (P) qua AC và vuông góc với mặt phẳng (SAD) chia khối chóp S.ABCD thành hai khối đa diện. Tỉ lệ thể tích hai khối đa diện là gần nhất với giá trị nào trong các giá trị sau
A. 0,11.
B. 0,13.
C. 0,7.
D. 0,9.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với
A
B
6
,
A
D
3
tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai mặt phẳng (SAB), (SAC) tạo với nhau góc
α
thỏa mãn
α
3
4
và cạnh SC 3. Thể tích khối S.ABCD bằng A. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với A B = 6 , A D = 3 tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai mặt phẳng (SAB), (SAC) tạo với nhau góc α thỏa mãn α = 3 4 và cạnh SC= 3. Thể tích khối S.ABCD bằng
A. 4 3
B. 8 3
C. 3 3
D. 5 3 3
Cho khối chóp tứ giác đều S.ABCD, gọi
α
mặt phẳng qua A và vuông góc SC. Biết rằng diện tích thiết diện tạo bởi
α
là hình chóp bằng nửa diện tích đáy ABCD. Tính góc
φ
tạo bởi cạnh bên SC và mặt đáy. A.
φ
a
r
c
sin...
Đọc tiếp
Cho khối chóp tứ giác đều S.ABCD, gọi α mặt phẳng qua A và vuông góc SC. Biết rằng diện tích thiết diện tạo bởi α là hình chóp bằng nửa diện tích đáy ABCD. Tính góc φ tạo bởi cạnh bên SC và mặt đáy.
A. φ = a r c sin 33 + 1 8
B. φ = a r c sin 33 - 1 8
C. φ = a r c sin 29 + 1 8
D. φ = a r c sin 29 - 1 8
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a các mặt bên (SAB), (SAD) cùng vuông góc với mặt phẳng đáy, SAa; góc giữa đường thẳng SC và mặt phẳng (SAB) bằng a. Khi đó tan
α
nhận giá trị nào trong các giá trị sau:
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a các mặt bên (SAB), (SAD) cùng vuông góc với mặt phẳng đáy, SA=a; góc giữa đường thẳng SC và mặt phẳng (SAB) bằng a. Khi đó tan α nhận giá trị nào trong các giá trị sau:
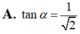
Cho hình chóp S. ABCD có đáy là ABCD là hình chữ nhật có AB a, BC 2a. Hai mp (SAB)và mp (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc
α
. Tính thể tích khối chóp S. ABCD theo
α
A.
2
a
3
15
3
B.
2
a
3...
Đọc tiếp
Cho hình chóp S. ABCD có đáy là ABCD là hình chữ nhật có AB = a, BC= 2a. Hai mp (SAB)và mp (SAD) cùng vuông góc với mặt phẳng đáy, cạnh SC hợp với mặt đáy một góc α . Tính thể tích khối chóp S. ABCD theo α
A. 2 a 3 15 3
B. 2 a 3 15
C. 2 a 3
D. 2 a 3 15 9