Đáp án D
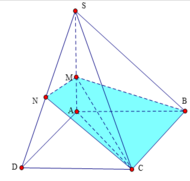
Ta có (BCM) cắt (SAD) theo giao tuyến MN//AD
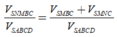
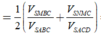


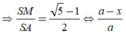

Đáp án D

Ta có (BCM) cắt (SAD) theo giao tuyến MN//AD
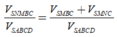
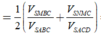


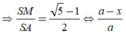

Hình chóp S.ABCD đáy là hình chữ nhật có AB =a, AD = 2a. SA vuông góc với mặt phẳng đáy, S A = a 3 . Thể tích khối chóp S.ABCD là
A. 2 a 3 6 3
B. a 3 3
C. 2 a 3 3 3
D. a 3 3 3
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt đáy (ABCD) và SA = a. Điểm M thuộc cạnh SA sao cho S M S K = k . Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau
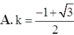
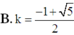
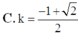
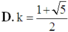
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a, SA vuông góc với mặt phẳng (ABCD), S A = a 3 . Thể tích của khối chóp S.ABC là:
A. 2 a 3 3 3
B. 2 a 3 3
C. a 3 3
D. a 3 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Cạnh SA vuông góc với đáy và SA=y Trên cạnh AD lấy điểm M sao cho AM=x Biết rằng x 2 + y 2 = a 2 Tìm giá trị lớn nhất của thể tích khối chóp S.ABCM.

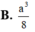
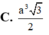
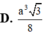
Cho hình chóp S.ABCD có đáy là hình chữ nhật với AB=2a, AD=3a. Cạnh bên SA vuông góc với đáy (ABCD), SA=a. Tính thể tích V của khối chóp S.ABCD.
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB= a 3 và AD = a . Đường thẳng SA vuông góc với mặt phẳng đáy và SA=a. Thể tích khối cầu ngoại tiếp hình chóp S.BCD bằng?
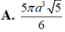
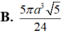
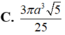
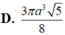
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB= BC= a AD=2 a ; SA vuông góc với mặt phẳng (ABCD) và SA =2a . Gọi M là một điểm trên cạnh AB; α là mặt phẳng đi qua M, vuông góc với AB. Đặt x= AM (0<x<a).
a.Tìm thiết diện của hình chóp S.ABCD với α . Thiết diện là hình gì?
b. Tính diện tích thiết diện theo a và x
Cho khối chóp S.ABCD có đáy ABCD là hình chữ nhật, A B = a 3 , AD=a, SA vuông góc với mặt đáy và mặt phẳng (SBC) tạo với đáy một góc 60 o . Tính thể tích V của khối cầu ngoại tiếp khối chóp S.ABCD.
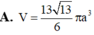
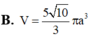
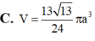
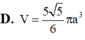
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = 2a. Biết SA vuông góc với mặt phẳng đáy và SA = 3a. Thể tích hình chóp S.ABCD là:
A. 6 a 3
B. 12 a 3
C. 2 a 3
D. 1 3 a 3