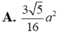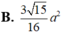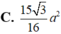Lời giải:
Gọi $Q$ là điểm nằm trên $DC$ sao cho $AD\parallel PQ$
Khi đó: $MN\parallel AD\parallel PQ$ nên $Q\in (MNP)$
$(MNPQ)$ chính là thiết diện của hình chóp cắt bởi $(MNP)$
Giờ ta cần tìm diện tích hình thang $MNPQ$
$SA=SD; DB=SC; AB=CD$ nên $\triangle SAB=\triangle SDC$
Tương ứng ta có $MP=NQ$
$MN=\frac{AD}{2}=\frac{3a}{2}$
$PQ=AD=3a$
$\Rightarrow MNPQ$ là hình thang cân.
Áp dụng định lý cos:
$\cos \widehat{SAB}=\frac{SA^2+AB^2-SB^2}{2SA.AB}=\frac{MA^2+AP^2-MP^2}{2MA.AP}$
$\Leftrightarrow \frac{9a^2+9a^2-27a^2}{2.3a.3a}=\frac{\frac{9}{4}a^2+4a^2-MP^2}{2.\frac{3}{2}a.2a}$
$\Rightarrow MP^2=\frac{37}{4}a^2$
$\Rightarrow h_{MNPQ}=\sqrt{MP^2-(\frac{PQ-MN}{2})^2}=\frac{\sqrt{139}}{4}a$
Diện tích thiết diện:
$S=\frac{MN+PQ}{2}.h=\frac{9\sqrt{139}}{16}a^2$