Đáp án D
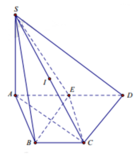
Gọi I là trung điểm của SC. Khi đó I là tâm mặt cầu đi qua các điểm S, A, B, C, E
Ta có: A C = a 2 + a 2 = a 2 , S C = a 2 2 + a 2 2 = 2 a
bán kính mặt cầu đi qua các điểm S, A, B, C, E là: R = S C 2 = a
Đáp án D

Gọi I là trung điểm của SC. Khi đó I là tâm mặt cầu đi qua các điểm S, A, B, C, E
Ta có: A C = a 2 + a 2 = a 2 , S C = a 2 2 + a 2 2 = 2 a
bán kính mặt cầu đi qua các điểm S, A, B, C, E là: R = S C 2 = a
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A, B. Biết S A ⊥ A B C D , A B = B C = a , A D = 2 a , S A = a 2 . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm S, A, B, C, E
A. a
B. a 6 3
C. a 3 2
D. a 30 6
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết S A ⊥ A B C D A B = B C = a ; A D = 2 a ; S A = a 2 . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.
A. a 3 2
B. a
C. a 6 3
D. a 30 6
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA=a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
A. a 41 8 .
B. a 41 24 .
C. a 41 16 .
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABCD) và SA = a. Gọi E là trung điểm của cạnh CD. Mặt cầu đi qua bốn điểm S, A, B, E có bán kính là
A. a 41 8
B. a 41 24
C. a 41 16
D. a 2 16
Cho hình chóp S.ABCD có SA vuông góc với đáy; S A = a 6 . Đáy ABCD là hình thang vuông tại A và B, A B = B C = 1 2 A D = a . Gọi E là trung điểm AD. Tính bán kính mặt cầu ngoại tiếp hình chóp S.ECD
A. R = a 30 3
B. R = a 19 6
C. R = a 6
D. R = 114 6 a .
Trong không gian Oxyz , gọi (S ) là mặt cầu đi qua D(0;1; 2) và tiếp xúc với các trục Ox,Oy,Oz tại các điểm A(a,0,0), B(0,b,0), C(0,0,c), trong đó a,b,c ∈ R \ 0 ; 1 . Tính bán kính của (S )?
A. 3 2 2
B. 5
C. 5 2
D. 5 2
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với 𝐴𝐵=𝐴𝐷=1, 𝐶𝐷=2. Cạnh bên SD vuông góc với mặt đáy, còn cạnh bên SA tạo với mặt đáy một góc 45°. Gọi E là trung điểm của cạnh CD. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.BCE.
A. R = 3 2
B. R = 14 2
C. R = 5 2
D. R = 11 2
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S trên mặt đáy (ABCD) trùng với trung điểm AB. Biết AB = a, BC = 2a, BD = a 10 . Góc giữa hai mặt phẳng (SBD) và mặt phẳng đáy là 600. Tính thể tích V của khối chóp S.ABCD theo a
A. V = 3 30 a 3 8
B. V = 30 a 3 4
C. V = 30 a 3 12
D. V = 30 a 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A , D , AD = DC = a , AB = 2a (a > 0) Hình chiếu của S lên mặt đáy trùng với trung điểm I của AD. Thể tích khối chóp S.IBC biết góc giữa SC và mặt đáy bằng 60 °
A. m = - 3
B. m = - 1 2
C. m = 1 2
D. m = 1