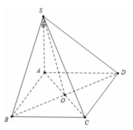
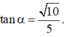cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh a, cạnh bên SA vuông góc với mặt đáy và SA = a
a) xác định và tính góc giữa SB và (ABCD)
b) xác định và tính góc giữa SD và (ABCD)
c) xác định và tính góc giữa SC và (ABCD)
d) xác định và tính góc giữa SO và (ABCD)
e) xác định và tính góc giữa SC và (SAB)
a.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=1\Rightarrow\widehat{SBA}=45^0\)
b.
\(SA\perp\left(ABCD\right)\Rightarrow AD\) là hình chiếu của SD lên (ABCD)
\(\Rightarrow\widehat{SDA}\) là góc giữa SD và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=1\Rightarrow\widehat{SDA}=45^0\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=AB\sqrt{2}=a\sqrt{2}\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{1}{\sqrt{2}}\Rightarrow\widehat{SCA}\approx35^016'\)
d.
\(SA\perp\left(ABCD\right)\Rightarrow AO\) là hình chiếu của SO lên (ABCD)
\(\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\Rightarrow tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{2}\Rightarrow\widehat{SOA}\approx54^044'\)
e.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow SB\) là hình chiếu của SC lên (SAB)
\(\Rightarrow\widehat{CSB}\) là góc giữa SC và (SAB)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{2}\Rightarrow tan\widehat{CSB}=\dfrac{BC}{SB}=\dfrac{1}{\sqrt{2}}\)
\(\Rightarrow\widehat{CSB}\approx35^016'\)