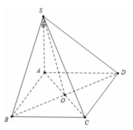
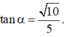cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh cạnh bên SA vuông góc với mặt đáy và SA = \(a\sqrt{6}\)
a) xác định và tính góc giữa SA và (ABCD)
b) xác định và tính góc giữa SD và (ABCD)
c) xác định và tính góc giữa SC và (ABCD)
d) xác định và tính góc giữa SO và (ABCD)
e) xác định và tính góc giữa SC và (SAB)
a: SA\(\perp\)(ABCD)
=>\(\widehat{SA;\left(ABCD\right)}=90^0\)
b: \(\widehat{SD;\left(ABCD\right)}=\widehat{DS;DA}=\widehat{SDA}\)
Xét ΔSAD vuông tại A có \(tanSDA=\dfrac{SA}{AD}=\sqrt{3}\)
nên \(\widehat{SDA}=60^0\)
=>\(\widehat{SD;\left(ABCD\right)}=60^0\)
c: \(\widehat{SC;\left(ABCD\right)}=\widehat{CS;CA}=\widehat{SCA}\)
ABCD là hình vuông
=>\(AC=\sqrt{AD^2+DC^2}=\sqrt{\left(a\sqrt{2}\right)^2+\left(a\sqrt{2}\right)^2}=2a\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{6}}{2a}=\dfrac{\sqrt{6}}{2}\)
nên \(\widehat{SCA}\simeq50^046'\)
=>\(\widehat{SC;\left(ABCD\right)}\simeq50^046'\)
d: \(\widehat{SO;\left(ABCD\right)}=\widehat{OS;OA}=\widehat{SOA}\)
O là trung điểm của AC
=>\(AO=\dfrac{AC}{2}=a\)
Xét ΔSAO vuông tại A có \(tanSOA=\dfrac{SA}{AO}=\sqrt{6}\)
nên \(\widehat{SOA}\simeq67^047'\)
=>\(\widehat{SO;\left(ABCD\right)}\simeq67^047'\)
e: CB\(\perp\)AB
CB\(\perp\)SA(SA\(\perp\)(ABCD))
SA,AB cùng thuộc mp(SBA)
Do đó: CB\(\perp\)(SAB)
=>\(\widehat{SC;\left(SAB\right)}=\widehat{SC;SB}=\widehat{CSB}\)
ΔSAC vuông tại A
=>\(SA^2+AC^2=SC^2\)
=>\(SC=\sqrt{\left(a\sqrt{6}\right)^2+\left(2a\right)^2}=a\sqrt{10}\)
ΔSAB vuông tại A
=>\(SA^2+AB^2=SB^2\)
=>\(SB=\sqrt{\left(a\sqrt{6}\right)^2+\left(a\sqrt{2}\right)^2}=a\sqrt{8}\)
Xét ΔBSC có \(BS^2+BC^2=SC^2\)
nên ΔBSC vuông tại B
Xét ΔBSC vuông tại B có \(sinCSB=\dfrac{CB}{SC}=\dfrac{a\sqrt{2}}{a\sqrt{10}}=\dfrac{1}{\sqrt{5}}\)
nên \(\widehat{CSB}\simeq24^05'\)
=>\(\widehat{SC;\left(SAB\right)}\simeq24^05'\)