a: (SC;(ABCD))=(CS;CA)=góc SCA
AC=2a*căn 2
tan SCA=SA/AC=3/2căn 2
=>góc SCA=47 độ
b: AH=SA*AB/SB=3a*2a/(a*căn 13)=6/căn 13*a
AK=SA*AC/SC=(3a*2a*căn 2)/(a*căn 17)=a*(6căn 2/căn 17)
cho hình chóp S.ABCD có đáy hình vuông cạnh a, SA = a, SA ⊥ (ABCD). Gọi H, K lần lượt là trung điểm của cạnh SB,SD; O là tâm hình vuông ABCD.
1/ Chứng minh: (SAB) ⊥ (SBC)
2/ Chứng minh: SC ⊥ (AHK)
Cho hình chóp S.ABCD có SA ⊥ (ABCD), SA = 2a, ABCD là hình vuông cạnh bằng a. Gọi O là tâm của ABCD, tính khoảng cách từ O đến SC.
A. a 3 3
B. a 3 4
C. a 2 3
D. a 2 4
Có hình chóp S. ABCD có đáy là hình vuôn cạnh a . SA vuông góc (ABCD) và SA= a căn6/3
a. Chứng minh CD vuông góc (SAD)
b. P, Q lần lượt là hình chiếu vuông góc của A lên SB , SD . chứng minh PQ vuông góc SC
C. Tính góc SC và (ABCD)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Cạnh bên SA vuông góc với mặt đáy. Gọi H,K lần lượt là hình chiếu của A lên SC; SD. Dựng KN // CD, với N ∈ SC. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Góc giữa hai mặt phẳng (SAC); (SAD) là góc HAK.
B. Góc giữa hai mặt phẳng (SCD); (SAD) là góc AKN.
C. Góc giữa hai mặt phẳng (SBC); (ABCD) là góc BSA.
D. Góc giữa hai mặt phẳng (SCD) và (ABCD) là góc SCB.
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB = a 2 và SA=SB=SC=SD=2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
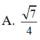
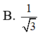
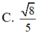
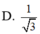
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc (ABCD). AH, AK lần lượt là đường cao của tam giác SAB, SAD.
a/ C/m: CD vuông góc SD và AK vuông góc SC.
b/ C/m: SC vuông góc (AHK).
c) Tính góc giữa SO với (ABCD)
d) Tính góc giữa SO với (SAB)
e) Tính khoảng cách từ B đến (SCD)
f) Tính khoảng cách từ H đến (SAC)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ ( A B C D ) Kẻ A H ⊥ S B ; A K ⊥ S D . Mặt phẳng (AHK) cắt SC tại I. Tính thể tích khối cầu ngoại tiếp khối ABCDIHK.
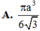
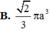
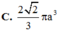
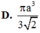
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a; SA=SB=SC=SD=a√2; O là tâm của hình vuông ABCD.
a) C/m (SAC) và (SBD) cùng vuông góc với (ABCD).
b) C/m (SAC) ⊥(SBD)
c) Tính khoảg cách từ S đến (ABCD)
d) Tính góc giữa đường SB và (ABCD).
e) Gọi M là trung điểm của CD, hạ OH⊥SM, chứng minh H là trực tâm tam giác SCD
f) Tính góc giưa hai mặt phẳng (SCD) và (ABCD)
g) Tính khoảng cách giữa SM và BC; SM và AB.
cần giải gấp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh = a, SA vuông góc (ABCD). Kẻ AH vuông góc SB, AK vuông góc SB.
a) BC vuông góc (SAB)
b) AH vuông góc SC
c) Gọi M là giao điểm của SC với (AHK). CM: HK vuông góc với AM
d) AH=?, HK=? biết SA=a\(\sqrt{3}\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a , SA vuông góc ABCD , SA =a√2
a) CM : BD vuông góc SAC
b) tính góc giữa SC và mp ABCD
