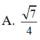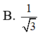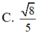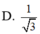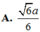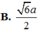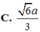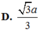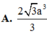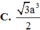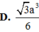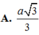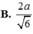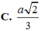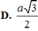\(AB||CD\Rightarrow AB||\left(SCD\right)\)
\(\Rightarrow d\left(AB;SD\right)=d\left(AB;\left(SCD\right)\right)=d\left(A;\left(SCD\right)\right)\)
Từ A kẻ \(AH\perp SD\) (H thuộc SD) \(\Rightarrow AH\perp\left(SCD\right)\)
\(\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(AD=BC=\sqrt{AC^2-AB^2}=a\)
Hệ thức lượng: \(AH=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\dfrac{2a\sqrt{5}}{5}\)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB = a 2 và SA=SB=SC=SD=2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB=BC=a, AD=2a vuông góc với mặt phẳng đáy và SA=a. Tính theo a khoảng cách giữa hai đường thẳng AC và SD
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a, SA=3a và SA vuông góc với mặt đáy. Góc giữa đường thẳng SD và mặt phẳng (ABCD) là
A. S A D ^
B. A S D ^
C. S D A ^
D. B S D ^
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AD=2a. Cạnh bên SA=2a và vuông góc với đáy. Tính khoảng cách giữa hai đường thẳng AB và SD
A. a
B. 2a
C. 2 a 5
D. a 2
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy, AB=a, AD=2a. Khoảng cách giữa hai đường thẳng AB và SD bằng a 3 Thể tích khối chóp S.ABCD bằng
cho hình chóp SABCD đáy ABCD là hình chữ nhật AB= a ,AD=2a,SA=SB=SC=SD=2a gọi O là giao điểm của AC và BD
a chứng minh mặt phẳng SAC vuông góc với mặt phẳng ABCD
b tính khoảng cách từ O->mặt phẳng SCD
c gọi M,N lần lượt là trung điểm của các cạnh SA và BC tính sin góc MN,CSBD
Cho hình chóp SABCD. Đáy là hình vuông cạnh 2a; SA= a căn 5. SA vuông góc với đáy a) Tính góc giữa SC và (SAD); góc giữa SB và (SAC) b)Tính góc giữa (SBC) và (ABCD) c)Tính khoảng cách từ SD đến BC
Cho hình chóp SABCD. Đáy là hình vuông cạnh 2a; SA= a căn 5. SA vuông góc với đáy a) Tính góc giữa SC và (SAD); góc giữa SB và (SAC) b)Tính góc giữa (SBC) và (ABCD) c)Tính khoảng cách từ SD đến BC
Cho hình chóp S.ABCD, đáy ABCD là hình chữ nhật. Cạnh SA vuông góc với mặt phẳng (ABCD). Biết AB = a, AD = 2a, góc giữa cạnh bên SD và mp (ABCD) bằng 60 ° . Tính khoảng cách từ A đến mp (SBD).
cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB=a, AD=2a , SA=3a và SA vuông góc với (ABCD). Tính góc giữa SD và mặt phẳng ABCD
