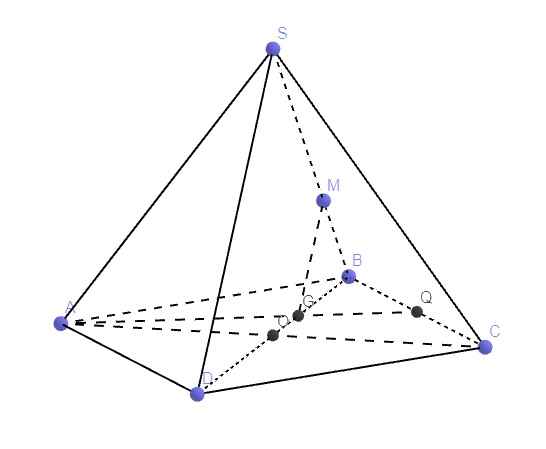
Gọi O là giao điểm AC và BD \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow\) G là trọng tâm tam giác ABC
\(\Rightarrow BG=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\)
\(\Rightarrow\dfrac{BG}{BD}=\dfrac{1}{3}\)
Lại có: \(SM=2MB\Rightarrow2MB=SB-MB\Rightarrow MB=\dfrac{1}{3}SB\Rightarrow\dfrac{MB}{SB}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{BG}{BD}=\dfrac{BM}{SB}=\dfrac{1}{3}\Rightarrow MG||SD\) (Talet đảo)
Mà \(SD\in\left(SAD\right)\Rightarrow MG||\left(SAD\right)\)