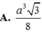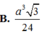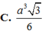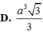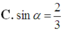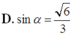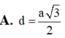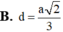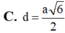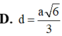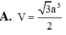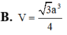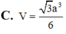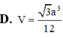Question

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy, SA = a, góc giữa mặt bên (SBC) và đáy bằng 60°. Tính thể tích khối chóp S.ABC theo a, biết khoảng cách từ C đến mặt phẳng (SAB) bằng 2a.

Answer 1

\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)

\(\Rightarrow BC=d\left(C;\left(SAB\right)\right)\Rightarrow BC=2a\)

Cũng từ \(BC\perp\left(SAB\right)\) mà \(BC=\left(SBC\right)\cap\left(ABC\right)\)

\(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và đáy

\(\Rightarrow\widehat{SBA}=60^0\)

\(\Rightarrow AB=\dfrac{SA}{tan60^0}=\dfrac{a\sqrt{3}}{3}\)

\(V=\dfrac{1}{3}.SA.\dfrac{1}{2}AB.BC=\dfrac{a^3\sqrt{3}}{9}\)