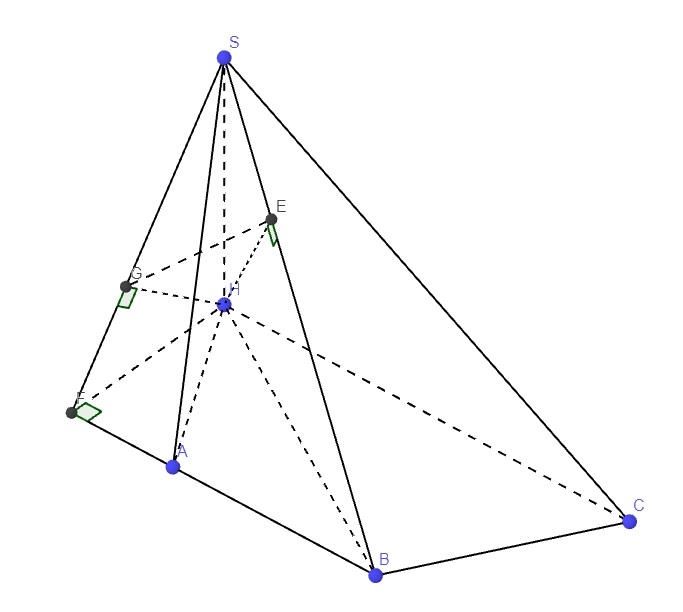
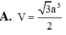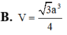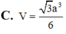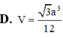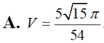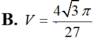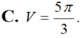Cho hình chóp S>ABC có đáy ABC là tam giác cân tại B với AB=BC=3, `\hat{ABC}=120^o`. Hình chiếu vuông góc H của S lên mặt phẳng (ABC) nằm trên tia Cx song song với AB, cùng phía với A trong nửa mặt phẳng bờ BC thỏa mãn `\hat{AHC}=60^o`. Biết cosin của góc giữa 2 mặt phẳng (SAB) và (SBC) bằng `sqrt10/5`. Tính thể tích khối chóp S.ABC
\(\widehat{BAH}=180^0-\widehat{AHC}=120^0=\widehat{ABC}\)
\(\Rightarrow ABCH\) là hình thang cân \(\Rightarrow AH=BC=3\); định lý hàm cos \(\Rightarrow AC=BH=3\sqrt{3}\)
\(\widehat{HBC}=90^0\) \(\Rightarrow BC\perp\left(SHB\right)\)
Từ H kẻ \(HE\perp SB\Rightarrow HE\perp\left(SBC\right)\)
Từ H kẻ HF vuông góc AB, từ H kẻ \(HG\perp SF\Rightarrow HG\perp\left(SAB\right)\)
\(\Rightarrow\widehat{EHG}\) là góc giữa (SAB) và (SBC)
\(HF=AH.cos30^0=\dfrac{3\sqrt{3}}{2}\) ; \(AF=AH.sin30^0=\dfrac{3}{2}\Rightarrow BF=AB+AF=\dfrac{9}{2}\)
Đặt \(SH=x\Rightarrow HG=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{3x\sqrt{3}}{\sqrt{4x^2+27}}\)
\(SG=\sqrt{SH^2-HG^2}=\sqrt{x^2-\dfrac{27x^2}{4x^2+27}}=\dfrac{2x^2}{\sqrt{4x^2+27}}\)
\(SB=\sqrt{SH^2+BH^2}=\sqrt{x^2+27}\)
\(HE=\dfrac{SH.BH}{\sqrt{SH^2+BH^2}}=\dfrac{3x\sqrt{3}}{\sqrt{x^2+27}}\)
\(EG=\dfrac{BF.SG}{SB}=\dfrac{9x^2}{\sqrt{\left(4x^2+27\right)\left(x^2+27\right)}}\)
\(\Rightarrow\dfrac{\sqrt{10}}{5}=\dfrac{HE^2+HG^2-EG^2}{2HE.HG}=\sqrt{\dfrac{x^2+27}{4x^2+27}}\)
\(\Rightarrow x=3\sqrt{3}\)
Tính chay đến đoạn tìm ra \(cos\alpha=\sqrt{\dfrac{x^2+27}{4x^2+27}}\) thì nhận ra cái căn nó đúng bằng \(\dfrac{SB}{2SF}\). Sau đó ngồi gần 1 tiếng để nghĩ cách chứng minh \(cos\alpha=\dfrac{SB}{2SF}\) để coi có được ko và kết quả là phí 1 tiếng :D