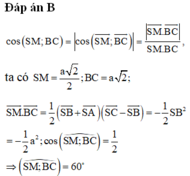Các câu hỏi tương tự
cho hình chóp S.ABC, SA vuông góc (ABC) đáy là tam giác ABC đều cạnh a và SA \(=a\sqrt{3}\)
a) tính góc giữa đường thẳng SB và AB
b) tính góc giữa đường thẳng SC và AC
c) M là trung điểm BC. Tính góc giữa đường thẳng SM và AM
Cho hình chóp S.ABCD có SAa, SB2a, SC3a,
A
S
B
^
B
S
C
^
60
°
,
C
S
A
^
90
°
. Gọi α là góc giữa hai đường thẳng SA và BC. Tính cos α. A.
cos
α...
Đọc tiếp
Cho hình chóp S.ABCD có SA=a, SB=2a, SC=3a, A S B ^ = B S C ^ = 60 ° , C S A ^ = 90 ° . Gọi α là góc giữa hai đường thẳng SA và BC. Tính cos α.
A. cos α = 7 7
B. cos α = - 7 7
C. cos α = 0
D. cos α = 2 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật biết AB=a; AD= 2a; SA vuông góc với đáy, SA=a√2. Xác định và tính góc giữa. a) Các đường thẳng SB, SC, SD với mp đáy. b) SC với các mp (SAD) và ( SAB). c) SA với mp (SCD). d) SB và (SAC).
Cho hình chóp S.ABCD có đáy là hình vuông; SA SB a và SA vuông góc (ABCD) Gọi M là trung điểm AD, tính khoảng cách giữa hai đường thẳng SC và BM A.
a
14
6
B.
6
a
14
C.
a
14
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông; SA = SB = a và SA vuông góc (ABCD) Gọi M là trung điểm AD, tính khoảng cách giữa hai đường thẳng SC và BM
A. a 14 6
B. 6 a 14
C. a 14 2
D. 2 a 14
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và SA a, SB 2a, SC 3a. Khoảng cách từ điểm S đến mặt phẳng (ABC) là A.
5
a
6
B.
6
a
7
C.
7
a
6
D.
6...
Đọc tiếp
Cho hình chóp S.ABC có các cạnh SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = 2a, SC = 3a. Khoảng cách từ điểm S đến mặt phẳng (ABC) là
A. 5 a 6
B. 6 a 7
C. 7 a 6
D. 6 a 5
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB a
2
và SASBSCSD2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB = a 2 và SA=SB=SC=SD=2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
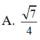
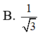
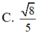
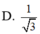
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SASBSCa. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
Đọc tiếp
Cho hình chóp S.ABC với SA⊥SB, SB⊥SC, SC⊥SA, SA=SB=SC=a. Gọi B′,C′ lần lượt là hình chiếu vuông góc của S trên AB,AC. Thể tích của hình chóp S.AB′C′ là
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có SA, SB,SC đôi một vuông góc. Gọi M là trung điểm của BC. CMR
a) \(SA\perp BC\)
b) \(SA\perp SM\)
Cho hình chóp A.ABC có SA = SB = SC = AB = AC = a và BC = a√2. Tính góc giữa hai đường thẳng AB và SC.