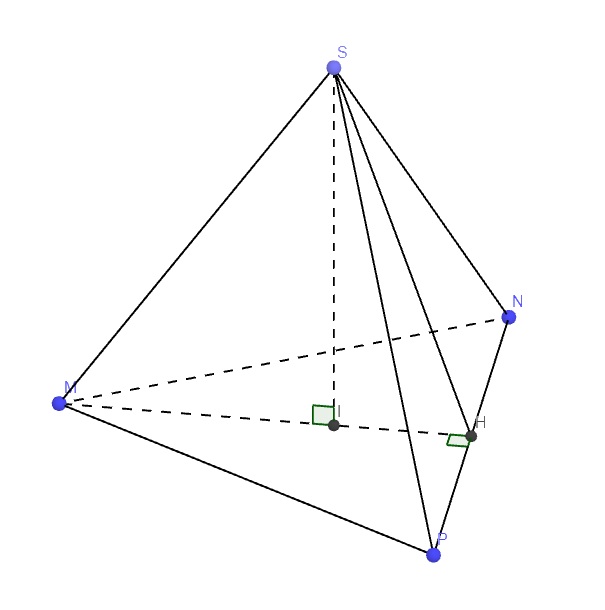
Tam giác MNP đều \(\Rightarrow MH\perp NP\)
Chóp S.MNP đều và I là tâm đáy \(\Rightarrow SI\perp\left(MNP\right)\)
\(\Rightarrow SI\perp IH\) hay tam giác SIH vuông tại I
Chóp S.MNP đều \(\Rightarrow\Delta SNP\) cân tại S \(\Rightarrow SH\) là trung tuyến kiêm đường cao
\(\Rightarrow SH\perp NP\)
a.
MNP đều \(\Rightarrow\widehat{N}=60^0\)
\(\Rightarrow MH=MN.sin\widehat{N}=4a.sin60^0=2a\sqrt{3}\)
b.
\(S_{\Delta MNP}=\dfrac{1}{2}MH.NP=\dfrac{1}{2}.2a\sqrt{3}.4a=4a^2\sqrt{3}\)
c.
\(NH=\dfrac{1}{2}NP=2a\)
Pitago tam giác vuông SNH: \(SH=\sqrt{SN^2-NH^2}=\sqrt{\left(6a\right)^2-\left(2a\right)^2}=4a\sqrt{2}\)
d.
\(S_{\Delta SNP}=\dfrac{1}{2}SH.NP=8a^2\sqrt{2}\)
e.
I là trọng tâm MNP \(\Rightarrow IH=\dfrac{1}{3}MH=\dfrac{2a\sqrt{3}}{3}\)
Pitago tam giác vuông SIH:
\(SI=\sqrt{SH^2-IH^2}=\dfrac{2a\sqrt{69}}{3}\)
Hình chóp tam giác đều là một hình chóp có đáy là tam giác đều, các mặt bên (cạnh bên) đều bằng nhau, và hình chiếu của đỉnh chóp xuống đáy trùng với tâm của tam giác đều 1. Hãy cùng giải quyết từng phần của bài toán:
a) Tính MH:
Gọi H là trung điểm của NP.Vì H là trung điểm, nên MH sẽ bằng một nửa của NP.Do đó, MH = NP / 2 = 2a.b) Tính diện tích đáy:
Đáy của hình chóp là tam giác đều, nên diện tích đáy là diện tích tam giác đều.Diện tích tam giác đều có công thức: S = (a^2 * √3) / 4 1.Vậy diện tích đáy là: Sđáy = (a^2 * √3) / 4.c) Tính độ dài NH, SH:
Đường cao được vẽ từ đỉnh của mỗi mặt bên của hình chóp đều gọi là trung đoạn của hình chóp đó 2.Vì H là trung điểm của NP, nên NH = NP / 2 = 2a.Do đó, SH = 2 * NH = 4a.d) Tính diện tích tam giác SNP:
Tam giác SNP là tam giác cân với SN = 6a.Diện tích tam giác cân có công thức: S = (1/2) * SN * NH.Thay giá trị: S = (1/2) * 6a * 2a = 6a^2.e) Tính chiều cao SI của hình chóp:
Chiều cao của hình chóp là đường cao từ đỉnh đến mặt đáy.Công thức tính chiều cao của tam giác đều: h = (a * √3) / 2 1.Vậy chiều cao của hình chóp là: SI = h = (a * √3) / 2.Hy vọng bạn đã hiểu rõ hơn về hình chóp tam giác đều và cách tính toán liên quan! 🌟