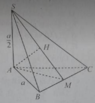
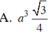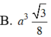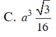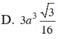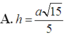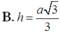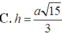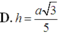Lời giải:
Gọi $O$ là tâm đáy thì $SO\perp (ABCD)$
Ta thấy:
$BO\perp AC, BO\perp SO\Rightarrow BO\perp (AC, SO)$
Hay $BO\perp (SAC)(*)$
Gọi $T$ là trung điểm $AB$, $OH\perp ST$.
$OT\perp AB$
$SO\perp AB$
$\Rightarrow (SOT)\perp AB$
$\Rightarrow OH\perp AB$
Mà $OH\perp ST$
$\Rightarrow OH\perp (AB, ST)$ hay $OH\perp (SAB)(**)$
Từ $(*); (**)\Rightarrow \cos a=\cos \widehat{HOB}$
Trong đó:
$BO=\frac{2\sqrt{2}}{2}=\sqrt{2}$
$SO=\sqrt{SB^2-BO^2}=\sqrt{(2\sqrt{2})^2-(\sqrt{2})^2}=\sqrt{6}$
$ST=\sqrt{SO^2+OT^2}=\sqrt{6+1}=\sqrt{7}$
$OH=\frac{SO.OT}{ST}=\frac{\sqrt{6}.1}{\sqrt{7}}=\sqrt{\frac{6}{7}}$
Vì $OH\perp (SAB)$ nên tam giác $BHO$ vuông tại $H$. Do đó:
$\cos a=\cos \widehat{HOB}=\frac{HO}{OB}=\frac{\sqrt{6}}{\sqrt{7}.\sqrt{2}}=\frac{\sqrt{3}}{\sqrt{7}}$