Cho hình bình hành MNPQ (MN > PQ) . Lấy điểm A trên canh MN , điểm B trên cạnh PQ sao cho AM = BP
a) Chứng minh rằng: MB // AP ,MB = AP .
b) Chứng minh rằng MB , NQ , AB đồng quy tại một điểm I .
c) Gọi H là giao điểm của MB và NQ . Tìm vị trí của A , B trên 2 cạnh MN , PQ của hình bình hành MNPQ để H là trọng tâm của tam giác MPQ .
d) Gọi C là giao điểm của 2 đường phân giác góc 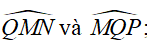
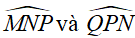
a: Xét tứ giác MAPB có
MA//PB
MA=PB
Do đó: MAPB là hình bình hành
=>MB//AP và MB=AP
b: Vì MAPB là hình bình hành
nen MP cắt BA tại trung điểm của mỗi đường(1)
Vì MNPQ là hình bình hành
nên MP cắt NQ tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra MP,BA,NQ đồng quy














