Nếu : f(x)=f(2) => f(2)=4.(2)+2=8+2=10
Nếu : f(-3)=f9-3)=>f(-3)=4.(-3)+2=-12+2=-10
f(2)= 4.2+2= 10
f(-3)= 4.(-3)+2= -10
tick nha ![]()
tui trả lời trước đó cao nguyễn uyên :))
f(2)=8+2=10
f(-3)=-12+2=-10
đúng đó tíh cho mình nhé bạn
Nếu : f(x)=f(2) => f(2)=4.(2)+2=8+2=10
Nếu : f(-3)=f9-3)=>f(-3)=4.(-3)+2=-12+2=-10
f(2)= 4.2+2= 10
f(-3)= 4.(-3)+2= -10
tick nha ![]()
tui trả lời trước đó cao nguyễn uyên :))
f(2)=8+2=10
f(-3)=-12+2=-10
đúng đó tíh cho mình nhé bạn
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Biết nguyên hàm của hàm số y = f ( x ) là F ( x ) = x 2 + 4 x + 1 . Khi đó f ( 3 ) bằng:
A. 6
B. 10
C. 22
D. 30
Cho hàm số y=f(x) có đạo hàm liên tục trên đoạn [-2;1] thỏa mãn f(0)=1 và f x 2 . f ' x = 3 x 2 + 4 x + 2 Giá trị lớn nhất của hàm số y=f(x) trên đoạn [-2;1] là
A. 2 16 3
B. 18 3
C. 16 3
D. 2 18 3
Cho hàm số y=f(x) có đồ thị hàm số y=f’(x) như hình bên dưới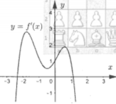
Hàm số g(x)=f(1-4x) đồng biến trên khoảng nào trong các khoảng sau?
![]()
![]()
![]()
Cho hàm số f(x) có f ' ( x ) = x 2 - 2 x , ∀ x ∈ R . Hàm số y = f ( 1 - x 2 ) + 4 x đồng biến trên khoảng nào dưới đây ?
A. - 6 ; 6
B. - ∞ ; 6
C. - 6 2 ; 6 2
D. - 6 2 ; + ∞
Cho hàm số y = f ( x ) có đạo hàm trên ℝ . Xét các hàm số g ( x ) = f x − f 2 x và h ( x ) = f ( x ) − f ( 4 x ) . Biết rằng g ' ( 1 ) = 18 và g ' ( 2 ) = 1000 . Tính h ' ( 1 ) :
A. − 2018
.
B. 2018
C. 2020
D. − 2020
Cho hàm số f(x) có đồ thị của hàm số y=f'(x) như hình vẽ bên và f(-2)=f(2)=0. Hàm số y = ( f ( 3 - x ) ) 2 nghịch biến trên khoảng nào dưới đây ?
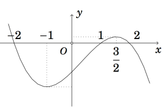
A. (1;2).
B. (-2;-1).
C. ( 5 ; + ∞ ) .
D. (2;5).
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5