Đáp án B.
f ( x ) = F ' ( x ) = 2 x + 4 ⇒ f ( 3 ) = 10
Đáp án B.
f ( x ) = F ' ( x ) = 2 x + 4 ⇒ f ( 3 ) = 10
Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(1)-F(2) bằng
A. ∫ 1 2 f x d x
B. ∫ 1 2 - f x d x
C. ∫ 2 1 - F x d x
D. ∫ 1 2 - F x d x
Gọi F ( x ) là một nguyên hàm cùa hàm số f ( x ) = x + 2 x - 1 . Biết rằng đồ thị hàm số F ( x ) đi qua điểm A ( 2 ; 3 ) . Khi đó F ( x ) là
A. F ( x ) = x + 3 ln | x - 1 | + 1
B. F ( x ) x + 3 ln | x - 1 | - 1
C. F ( x ) = x + 3 ln ( x - 1 )
D. F ( x ) = x + 3 ln ( x - 1 ) + 1
Cho hàm f x = x + 2 2 x 3 có nguyên hàm là hàm F(x). Biết F(1)=6. Khi đó F(x) có dạng:
A. ln x - 4 x - 2 x 2 + 6
B. ln x + 4 x - 2 x 2 + 4
C. ln x + 4 x - 2 x 2 + 4
D. ln x - 4 x - 2 x 2 + 6
Cho hàm số y = f (x) liên tục trên R có đồ thị như hình vẽ.
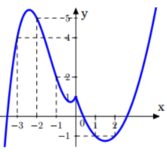
Biết trên ( - ∞ ; - 3 ) ∪ ( 2 ; + ∞ ) t h ì f ' ( x ) > 0 . Số nghiệm nguyên thuộc (-10; 10) của bất phương trình [ f ( x ) + x - 1 ] ( x 2 - x - 6 ) > 0 là
A. 9
B. 10
C. 8
D. 7
Biết hàm số F ( x ) = a x 3 + ( a + b ) x 2 + ( 2 a - b + c ) x + 1 là một nguyên hàm của hàm số f ( x ) = 3 x 2 + 6 x + 2 . Tổng a+b+c là:
A. 5
B. 4
C. 3
D. 2
Cho hàm số f x = a x + b c x + d với a , b , c , d ∈ R có đồ thị hàm số y=f'(x) như hình vẽ bên. Biết rằng giá trị lớn nhất của hàm số y=f(x) trên đoạn [-3;-2] bằng 8. Giá trị của f(2) bằng.

A. 2
B. 5
C. 4
D. 6
Cho hàm số y=f(x) có đạo hàm là
f ' ( x ) = ( x − 1 ) 2 ( x + 2 ) 3 ( 3 − x ) . Khi đó số điểm cực trị của hàm số là
A. 0
B. 1
C. 2
D. 3
Biết F (x) là một nguyên hàm của hàm số f ( x ) = 10 x 3 - 7 x + 2 2 x - 1 thỏa mãn F(1) = 5. Giả sử rằng F(3) = a + b 5 , trong đó a , b là các số nguyên. Tính tổng bình phương của a và b.
A. 121
B. 73
C. 265
D. 361
Cho hàm số y=f(x) có đạo hàm, liên tục trên đoạn [-3;3] và đồ thị hàm số y=f' (x) như hình vẽ bên. Biết f(1)=6 và g(x)=f(x)- ( x + 1 ) 2 2 .
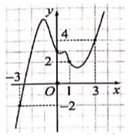
Kết luận nào sau đây là đúng
A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].
B. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].
C. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].
D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].