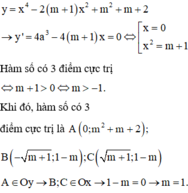Các câu hỏi tương tự
Cho hàm số
y
x
4
−
2
m
+
1
x
2
+
m
2
+
m
+
2
có đồ thị (C). Gọi A, B, C là ba điểm cực trị của (C) và
m
m
o
là giá trị thỏa mãn A, B, C đều thuộc các trục tọa độ, khi đó...
Đọc tiếp
Cho hàm số y = x 4 − 2 m + 1 x 2 + m 2 + m + 2 có đồ thị (C). Gọi A, B, C là ba điểm cực trị của (C) và m = m o là giá trị thỏa mãn A, B, C đều thuộc các trục tọa độ, khi đó m o gần giá trị nào nhất trong các giá trị sau?
A. -1.
B. -3.
C. 4.
D. 5.
Cho hàm số
y
9
x
4
+
m
−
4
x
2
−
m
+
1
có đồ thị (C). Biết
m
m
0
là giá trị để đồ thị (C) có ba...
Đọc tiếp
Cho hàm số y = 9 x 4 + m − 4 x 2 − m + 1 có đồ thị (C). Biết m = m 0 là giá trị để đồ thị (C) có ba điểm cực trị tạo thành tam giác đều. Khi đó giá trị m 0 gần giá trị nào nhất trong các giá trị sau:
A. -4
B. -1
C. 2
D. 5
Gọi S là tập tất cả giá trị của tham số m để đồ thị hàm số
y
x
4
-
2
m
+
1
x
2
+
m
có ba điểm cực trị A, B, C sao cho OABC ; trong đó O là gốc tọa độ, A là điểm cực trị trên trục tung và B, C là hai điểm cực trị còn lại. Tích của tất cả các phần tử trong tập S bằng A. 8 B. -8 C. 4 C. -4
Đọc tiếp
Gọi S là tập tất cả giá trị của tham số m để đồ thị hàm số y = x 4 - 2 m + 1 x 2 + m có ba điểm cực trị A, B, C sao cho OA=BC ; trong đó O là gốc tọa độ, A là điểm cực trị trên trục tung và B, C là hai điểm cực trị còn lại. Tích của tất cả các phần tử trong tập S bằng
A. 8
B. -8
C. 4
C. -4
Cho các số thực a, b, c, d thỏa mãn 0 a b c d và hàm số y f(x). Biết hàm số y f(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y f(x) trên
[
0
;
d
]
. Khẳng định nào sau đây là khẳng định đúng? A. M + m f(b) + f(a) B. M + m f(d) + f(c) C. M + m f(0) + f(c) D. M + m f(0) + f(a)
Đọc tiếp
Cho các số thực a, b, c, d thỏa mãn 0 < a < b < c < d và hàm số y = f(x). Biết hàm số y = f'(x) có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên [ 0 ; d ] . Khẳng định nào sau đây là khẳng định đúng?
A. M + m = f(b) + f(a)
B. M + m = f(d) + f(c)
C. M + m = f(0) + f(c)
D. M + m = f(0) + f(a)
Cho hàm số
y
x
4
−
3
m
x
x
−
2
m
2
+
m
4
có đồ thị (C), biết đồ thị (C) có 3 điểm cực trị A, B, C và ABCD là hình thoi, trong đó
D
0
;
−
3
thuộc trục tung. Khi đó các giá trị của tham s...
Đọc tiếp
Cho hàm số y = x 4 − 3 m x x − 2 m 2 + m 4 có đồ thị (C), biết đồ thị (C) có 3 điểm cực trị A, B, C và ABCD là hình thoi, trong đó D 0 ; − 3 thuộc trục tung. Khi đó các giá trị của tham số m thuộc khoảng nào dưới đây?
A. m ∈ − 1 ; 1 2 .
B. m ∈ 2 ; 3 .
C. m ∈ 9 5 ; 2 .
D. m ∈ 1 2 ; 9 5 .
Xét các khẳng định sau:(I). Nếu hàm số y f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M m (II). Đồ thị hàm số
y
a
x
4
+
b
x
2
+
c
(
a
≠
0...
Đọc tiếp
Xét các khẳng định sau:
(I). Nếu hàm số y = f(x) có giá trị cực đại là M và giá trị cực tiểu là m thì M > m
(II). Đồ thị hàm số y = a x 4 + b x 2 + c ( a ≠ 0 ) luôn có ít nhất một điểm cực trị
(III). Tiếp tuyến (nếu có) tại một điểm cực trị của đồ thị hàm số luôn song song với trục hoành.
Số khẳng định đúng là :
A. 0
B. 3
C. 2
D. 1
Cho hàm số
y
x
−
m
2
x
+
1
(với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S 1? A. Hai B. Ba C. Một D. Không
Đọc tiếp
Cho hàm số y = x − m 2 x + 1 (với m là tham số khác 0) có đồ thị là (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?
A. Hai
B. Ba
C. Một
D. Không
Cho hàm số
y
x
4
−
2
m
+
1
x
2
+
m
có đồ thị (C), m là tham số. (C) có ba điểm cực trị A, B, C sao cho OAOB; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung khi: A.
m
0
hoặc
m
2
B.
m...
Đọc tiếp
Cho hàm số y = x 4 − 2 m + 1 x 2 + m có đồ thị (C), m là tham số. (C) có ba điểm cực trị A, B, C sao cho OA=OB; trong đó O là gốc tọa độ, A là điểm cực trị thuộc trục tung khi:
A. m = 0 hoặc m = 2
B. m = 2 ± 2 2
C. m = 3 ± 3 3
D. m = 5 ± 5 5
Cho hàm số y
x
-
m
2
x
+
1
(với m là tham số khác 0) có đồ thị (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S 1? A. 0. B. 1 C. 2 D. 3.
Đọc tiếp
Cho hàm số y = x - m 2 x + 1 (với m là tham số khác 0) có đồ thị (C). Gọi S là diện tích hình phẳng giới hạn bởi đồ thị (C) và hai trục tọa độ. Có bao nhiêu giá trị thực của m thỏa mãn S = 1?
A. 0.
B. 1
C. 2
D. 3.