Đáp án D
Ta có
![]()
Mặt khác
![]()
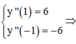
Tọa độ cực tiểu của đồ thị hàm số là (1;0)
Đáp án D
Ta có
![]()
Mặt khác
![]()
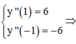
Tọa độ cực tiểu của đồ thị hàm số là (1;0)
Tìm m để đồ thị hàm số y = x 4 - 2 m + 1 x 2 + m có ba điểm cực trị A; B; C sao cho OA = BC , trong đó O là gốc tọa độ; A là điểm cực đại, B và C là hai điểm cực tiểu của đồ thị hàm số.
A. m = 2 ± 2 2
B. m = 2 ± 2
C. m = 2 ± 2 3
D. m = 2 + 2 2
Tìm m để đồ thị hàm số y = x 4 - 2 m + 1 x 2 + m có ba điểm cực trị A, B, C sao cho OA = OB trong đó O là gốc tọa độ, A là điểm cực đại, B và C là hai điểm cực tiểu của đồ thị hàm số
A. m = 2 ± 2 2
B. m = 2 ± 2
C. m = 2 ± 2 3
D. m = 2 + 2 2
Cho hàm số y = x 3 - 3 x + 2 . Tọa độ điểm cực tiểu của đồ thị hàm số là
A. (-2;0)
B. (-1;4)
C. (0;1)
D. (1;0)
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: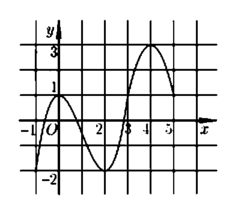
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Cho hàm số y = x^3 -3x. Tọa độ của điểm cực đại của đồ thị hàm số là:
A. ( - 2 ; 1 )
B. - 1 ; 2
C. 3 ; 2 3
D. 1 ; - 2
Cho hàm số y = x 4 + a x 2 + b . Biết rằng đồ thị hàm số nhận điểm A(-1;4) là điểm cực tiểu. Tổng 2a + b bằng:
A. -1
B. 1
C. 2
D. 0
Cho hàm số y = f ( x ) = x 3 + a x 2 + b x + c đạt cực tiểu bằng – 3 tại điểm x=1 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2. Tính đạo hàm cấp một của hàm số tại x= -3
A. f'(-3)= 0
B. f'(-3)= 2
C. f'(-3)= 1
D. f'(-3)= -2
Cho hàm số f(x) có đồ thị (C) như hình vẽ. Tọa độ điểm cực tiểu của (C) là
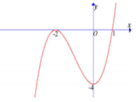
A. (0;-2)
B. (0;-4)
C. (1;0)
D. (-2;0)
Cho hàm số y = x 3 3 - 2 x 2 + 3 x + 2 3 . Tọa độ điểm cực tiểu của đồ thị hàm số là
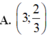
B. (1; -2)
C. (1; 2)
D. (-1; 2)