Các câu hỏi tương tự
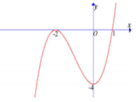
Cho hàm số y f(x) (ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là A. x – 3y +2 0 B. x + 3y +2 0 C. x – 3y - 2 0 D. x + 3y -2 0
Đọc tiếp
Cho hàm số y = f(x) =(ax+b)/(cx+d)(a,b,c,d ϵ R;c ≠ 0;d ≠ 0) có đồ thị (C). Đồ thị của hàm số y = f’(x) như hình vẽ dưới đây. Biết (C) cắt trục tung tại điểm có tung độ bằng 2. Tiếp tuyến của (C) tại giao điểm của (C) và trục hoành có phương trình là

A. x – 3y +2 = 0
B. x + 3y +2 = 0
C. x – 3y - 2 = 0
D. x + 3y -2 = 0
Cho hàm số
y
f
x
ax
3
+
bx
2
+
cx
+
d
có đồ thị (C), đồ thị y f (x) như hình vẽ bên. Biết đồ thị hàm số y f(x) có điểm cực tiểu có tung độ bằng
2
3
. Tính ...
Đọc tiếp
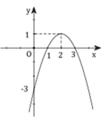
Cho hàm số y = f x = ax 3 + bx 2 + cx + d có đồ thị (C), đồ thị y = f '(x) như hình vẽ bên. Biết đồ thị hàm số y = f(x) có điểm cực tiểu có tung độ bằng 2 3 . Tính 3 a − b + 5 c + 3 d bằng?
A. -16
B. -12
C. 9
D. 10
Cho hàm số
y
f
(
x
)
a
x
3
+
b
x
2
+
c
x
+
d
(a;b;c;d
∈
R, a
≠...
Đọc tiếp
Cho hàm số y = f ( x ) = a x 3 + b x 2 + c x + d (a;b;c;d ∈ R, a ≠ 0) có đồ thị (C). Biết rằng đồ thị (C) đi qua gốc tọa độ và có đồ thị hàm số y = f’(x) cho bởi hình vẽ sau đây.

Tính giá trị H = f(4) – f(2)
A. H = 51
B. H = 54
C. H = 58
D. H = 64
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
có hai cực trị
x
1
,
x
2
thỏa mãn
-
2
x
1
0
x
2...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 2 + c x + d có hai cực trị x 1 , x 2 thỏa mãn - 2 < x 1 < 0 < x 2 < 2 và có đồ thị như hình vẽ.
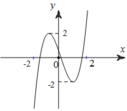
Số điểm cực tiểu của hàm số y = f(x) là
A. 3.
B. 5.
C. 7.
D. 4.
Cho hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
(với a,b,c,d ϵ ℝ và a≠0) có đồ thị như hình vẽ. Số điểm cực trị của hàm số
g
x
f
-
2
x
2
+
4...
Đọc tiếp
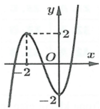
Cho hàm số f x = a x 3 + b x 2 + c x + d (với a,b,c,d ϵ ℝ và a≠0) có đồ thị như hình vẽ. Số điểm cực trị của hàm số g x = f - 2 x 2 + 4 x là
A. 2.
B. 3.
C. 4.
D. 5.
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x0, x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ) A.
2...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C) biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại 2 điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và 2 đường thẳng x=0, x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ)
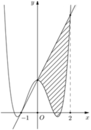
A. 2 5
B. 1 9
C. 2 9
D. 1 5
Cho hàm số
y
f
(
x
;
m
)
có đồ thị hàm số
y
f
(
x
;
m
)
như hình vẽ Biết
f
(
a
)
f
(
c
)
0
;
f
(
b
)
0
f
(
e
)
Hỏi hàm số...
Đọc tiếp
Cho hàm số y = f ( x ; m ) có đồ thị hàm số y = f ' ( x ; m ) như hình vẽ
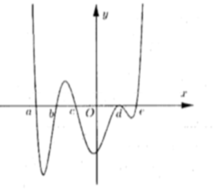
Biết f ( a ) > f ( c ) > 0 ; f ( b ) < 0 < f ( e ) Hỏi hàm số y = f ( x , m ) có bao nhiêu điểm cực trị?
A. 5
B. 7
C. 9
D. 10
Cho hàm số
y
f
(
x
)
có đồ thị như hình vẽ. Biết tất cả các điểm cực trị của hàm số
y
f
(
x
)
là – 2, 0, 2, a , 6 với 4 a 6. Số điểm cực trị của hàm số
y
f
(
x
6
−
3
x
2
)
là A. 8 B. 11 C. 9 D. 7
Đọc tiếp
Cho hàm số y = f ( x ) có đồ thị như hình vẽ.
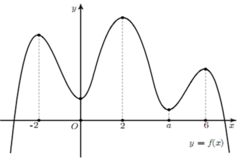
Biết tất cả các điểm cực trị của hàm số y = f ( x ) là – 2, 0, 2, a , 6 với 4 < a < 6. Số điểm cực trị của hàm số y = f ( x 6 − 3 x 2 ) là
A. 8
B. 11
C. 9
D. 7
Cho hàm số
y
a
x
4
+
b
x
2
+
c
có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x0; x2 có diện tích bằng
28
5
(phần gạch chéo trong hình vẽ). Diện tích hình phẳn...
Đọc tiếp
Cho hàm số y = a x 4 + b x 2 + c có đồ thị (C), biết rằng (C) đi qua điểm A(-1;0) tiếp tuyến d tại A của (C) cắt (C) tại hai điểm có hoành độ lần lượt là 0 và 2, diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=0; x=2 có diện tích bằng 28 5 (phần gạch chéo trong hình vẽ). Diện tích hình phẳng giới hạn bởi d, đồ thị (C) và hai đường thẳng x=-1; x=0 có diện tích bằng:

A. 2 5
B. 1 9
C. 2 9
D. 1 5