Đáp án B
y = x + 2 x + 1 có TCN: y = 1 và TCĐ: x = − 1
I − 1 ; 1 , M ∈ đồ thị ⇒ gọi M m ; m + 2 m + 1
⇒ I M → = m + 1 ; m + 2 m + 1 − 1
I M → = m + 1 ; 1 m + 1
I M = m + 1 2 + 1 m + 1 2 ≥ 2 m + 1 . 1 m + 1 (BĐT Cô si)
⇒ I M ≥ 2
GTNN của I M là 2 .
Đáp án B
y = x + 2 x + 1 có TCN: y = 1 và TCĐ: x = − 1
I − 1 ; 1 , M ∈ đồ thị ⇒ gọi M m ; m + 2 m + 1
⇒ I M → = m + 1 ; m + 2 m + 1 − 1
I M → = m + 1 ; 1 m + 1
I M = m + 1 2 + 1 m + 1 2 ≥ 2 m + 1 . 1 m + 1 (BĐT Cô si)
⇒ I M ≥ 2
GTNN của I M là 2 .
Cho hàm số y = x + 2 x − 2 có đồ thị là (C). Gọi I là giao điểm hai đường tiệm cận của (C). Tiếp tuyến của (C) cắt hai đường tiệm cận của (C) tại hai điểm A, B. Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác IAB bằng
A. 2 π
B. 8 π
C. 4 2 π
D. 4 π
Cho hàm số y = 2 x - 1 2 x - 2 có đồ thị (C). Gọi M x 0 ; y 0 (với x 0 > 1 ) là điểm thuộc (C), biết tiếp tuyến của (C) tại M cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho S ∆ O I B = 8 S ∆ O I A (trong đó O là gốc tọa độ, I là giao điểm hai tiệm cận). Giá trị của S = x 0 + 4 y 0 bằng
A. 8
B. 2
C. 17 4
D. 23 4
Cho hàm số ( C ) : y = x + 1 - x + 3 . Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số (C). Đường thẳng d : y = x + m cắt (C) tại hai điểm phân biệt A, B tạo thành tam giác ABI có trọng tâm nằm trên (C). Có hai giá trị của m thoả mãn yêu cầu bài toán. Tổng hai giá trị của m là:
A. 0
B. 2
C. –8
D. –10
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C). Gọi M là điểm bất kì thuộc đồ thị (C). Tiếp tuyến của đồ thị (C) tại M cắt hai tiệm cận của đồ thị (C) tại P và Q. Giá trị nhỏ nhất của đoạn thẳng PQ bằng
A. 3 2
B. 4 2
C. 2 2
D. 2
Tìm tọa độ điểm M có hoành độ dương thuộc đồ thị (C) của hàm số y = x + 2 x − 2 sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C) đạt giá trị nhỏ nhất.
A. M(1;-3)
B. M(3;5)
C. M(0;-1)
D. M(4;3)
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi I là giao điểm của hai tiệm cận, M là một điểm thuộc (C). Tiếp tuyến tại M của (C) cắt hai tiệm cận tại A và B. Phát biểu nào sau đây là sai?
A. M là trung điểm của AB
B. Diện tích tam giác IAB là một số không đổi
C. Tích khoảng cách từ M đến hai tiệm cận là một số không đổi
D. Tổng khoảng cách từ M đến hai tiệm cận là một số không đổi
Cho hàm số y = x + 3 x − 2 có đồ thị C . Gọi I là giao điểm của hai đường tiệm cận của C . Khi đó tọa độ của điểm I là
A. I − 3 ; 0 .
B. I 1 ; 2 .
C. I 2 ; 1 .
D. I 0 ; − 3 2 .
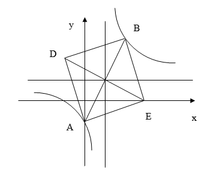
Cho hàm số y = f x = x + 1 x − 1 có đồ thị (C). Giả sử A, B là hai điểm nằm trên (C) đồng thời đối xứng nhau qua điểm I là giao điểm của hai đường tiệm cận của đồ thị (C). Dựng hình vuông AEBD . Tìm diện tích nhỏ nhất S min của hình vuông đó.
A. S min = 8 2
B. S min = 4 2
C. S min = 4
D. S min = 8
Tất cả các giá trị thực của tham số m để đường thẳng d : y = 2 x + m cắt đồ thị hàm số y = 2 x - 4 x - 1 tại hai điểm phân biệt A và B sao cho 4 S ∆ I A B = 15 , với I là giao điểm của hai đường tiệm cận của đồ thị (C) là
A. m = ± 5
B. m = 0
C. m = 5
D. m = - 5