Các câu hỏi tương tự
Cho hàm số
y
x
-
1
x
+
2
, gọi d là tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng m - 2. Biết đường thẳng d cắt tiệm cận đứng của đồ thị hàm số tại điểm A(x1;y1) và cắt tiệm cận ngang của đồ thị hàm số tại điểm B(x2;y2). Gọi S là tập hợp các số ...
Đọc tiếp
Cho hàm số y = x - 1 x + 2 , gọi d là tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng m - 2. Biết đường thẳng d cắt tiệm cận đứng của đồ thị hàm số tại điểm A(x1;y1) và cắt tiệm cận ngang của đồ thị hàm số tại điểm B(x2;y2). Gọi S là tập hợp các số m sao cho x2 + y1 = -5. Tính tổng bình phương các phần tử của S
A. 4
B. 0
C. 10
D. 9
Cho hàm số
y
2
x
-
1
x
+
1
có đồ thị là ( C). Gọi I là giao điểm 2 đường tiệm cận. Gọi
M
x
0
;
y
0
,
x
0
0...
Đọc tiếp
Cho hàm số y = 2 x - 1 x + 1 có đồ thị là ( C). Gọi I là giao điểm 2 đường tiệm cận. Gọi M x 0 ; y 0 , x 0 > 0 là một điểm trên (C) sao cho tiếp tuyến với (C) tại M cắt hai đường tiệm cận lần lượt tại A, B thỏa mãn A I 2 + I B 2 = 40 .Khi đó tích x 0 y 0 bằng.
A. 15 4
B. 1 2
C. 1
D. 2
Cho hàm số
y
2
x
-
1
x
+
1
có đồ thị là (C). Gọi I là giao điểm 2 đường tiệm cận. Gọi
M
x
0
,
y...
Đọc tiếp
Cho hàm số y = 2 x - 1 x + 1 có đồ thị là (C). Gọi I là giao điểm 2 đường tiệm cận. Gọi M x 0 , y 0 , x 0 > 0 là một điểm trên (C) sao cho tiếp tuyến với (C) tại M cắt hai đường tiệm cận lần lượt tại A, B thỏa mãn A B 2 + I B 2 = 40 . Khi đó tích x 0 y 0 bằng
A. 15 4
B. 1 2
C. 1
D. 2
Cho hàm số
y
2
x
-
1
2
x
-
2
có đồ thị (C). Gọi
M
x
0
;
y
0
(với
x
0
1
) là điểm thu...
Đọc tiếp
Cho hàm số y = 2 x - 1 2 x - 2 có đồ thị (C). Gọi M x 0 ; y 0 (với x 0 > 1 ) là điểm thuộc (C), biết tiếp tuyến của (C) tại M cắt tiệm cận đứng và tiệm cận ngang lần lượt tại A và B sao cho S ∆ O I B = 8 S ∆ O I A (trong đó O là gốc tọa độ, I là giao điểm hai tiệm cận). Giá trị của S = x 0 + 4 y 0 bằng
A. 8
B. 2
C. 17 4
D. 23 4
Cho hàm số
(
C
)
:
y
x
+
1
-
x
+
3
. Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số (C). Đường thẳng
d
:
y
x
+
m
cắt (C) tại hai điểm phân biệt A, B tạo thành tam giác ABI có trọn...
Đọc tiếp
Cho hàm số ( C ) : y = x + 1 - x + 3 . Gọi I là giao điểm của hai tiệm cận của đồ thị hàm số (C). Đường thẳng d : y = x + m cắt (C) tại hai điểm phân biệt A, B tạo thành tam giác ABI có trọng tâm nằm trên (C). Có hai giá trị của m thoả mãn yêu cầu bài toán. Tổng hai giá trị của m là:
A. 0
B. 2
C. –8
D. –10
Cho hàm số
y
2
x
-
1
x
+
1
có đồ thị (C). Gọi I là giao điểm hai đường tiệm cận, là một điểm trên (C) sao cho tiếp tuyến với (C) tại M cắt hai đường tiệm cận lần lượt là A, B thỏa mãn
I
A
2
+
I
B
2...
Đọc tiếp
Cho hàm số y = 2 x - 1 x + 1 có đồ thị (C). Gọi I là giao điểm hai đường tiệm cận, là một điểm trên (C) sao cho tiếp tuyến với (C) tại M cắt hai đường tiệm cận lần lượt là A, B thỏa mãn I A 2 + I B 2 = 40 . Tích x 0 y 0
A. 1 2
B. 2
C. 1
D. 15 4
Cho hàm số
y
x
+
2
x
−
2
có đồ thị là (C). Gọi I là giao điểm hai đường tiệm cận của (C). Tiếp tuyến của (C) cắt hai đường tiệm cận của (C) tại hai điểm A, B. Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác IAB bằng A.
2
π
B.
8
π
C.
4
2...
Đọc tiếp
Cho hàm số y = x + 2 x − 2 có đồ thị là (C). Gọi I là giao điểm hai đường tiệm cận của (C). Tiếp tuyến của (C) cắt hai đường tiệm cận của (C) tại hai điểm A, B. Giá trị nhỏ nhất của chu vi đường tròn ngoại tiếp tam giác IAB bằng
A. 2 π
B. 8 π
C. 4 2 π
D. 4 π
Cho hàm số
y
x
+
1
x
-
1
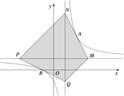
có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng A. 16. B. 32. C. 8. D. 4.
Đọc tiếp
Cho hàm số y = x + 1 x - 1 có đồ thị (C). Gọi A,B là hai điểm thuộc hai nhánh của (C) và các tiếp tuyến của (C) tại A,B cắt các đường tiệm cận ngang và đứng của (C) lần lượt tại các điểm M,N,P,Q (tham khảo hình vẽ bên). Diện tích tứ giác MNPQ có giá trị nhỏ nhất bằng
A. 16.
B. 32.
C. 8.
D. 4.
Cho hàm số
y
x
x
2
−
3
có đồ thị
C
. Có bao nhiêu điểm M thuộc đồ thị
C
thỏa mãn tiếp tuyến tại M của
C
cắt
C
và trục hoành lần lượt tại hai điểm phân biệt A (khác M) và B sao cho M là trung điểm của đoạn thẳng AB? A. 2 B. 1 C. 0 D. 3
Đọc tiếp
Cho hàm số y = x x 2 − 3 có đồ thị C . Có bao nhiêu điểm M thuộc đồ thị C thỏa mãn tiếp tuyến tại M của C cắt C và trục hoành lần lượt tại hai điểm phân biệt A (khác M) và B sao cho M là trung điểm của đoạn thẳng AB?
A. 2
B. 1
C. 0
D. 3




