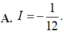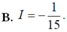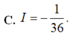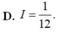Question

Cho hàm số f(x) liên tục trên đoạn [0;1] có f(1)=2 và \(\int_0^1f\left(x\right)dx=7\). Tính tích phân \(I=\int_0^1x\cdot f'\left(x\right)dx\)

A: I=-9

B: I=5

C: I=-5

D: I=9

Giải thích cách làm dạng này giúp em với ạ

 

Answer 1

Xét \(\int\limits^1_0x.f'\left(x\right)dx\)

Đặt \(\left\{{}\begin{matrix}u=x\\dv=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=f\left(x\right)\end{matrix}\right.\)

\(\Rightarrow I=x.f\left(x\right)|^1_0-\int\limits^1_0f\left(x\right)dx\)

\(=1.f\left(1\right)-0.f\left(0\right)-7=-5\)