Chọn A.
- Ta có: f(2) = m.
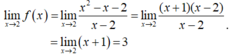
→ Hàm số liên tục tại điểm x = 2.
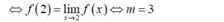
Chọn A.
- Ta có: f(2) = m.
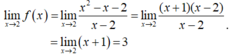
→ Hàm số liên tục tại điểm x = 2.
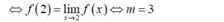
Cho hàm số: f x = 3 x - 5 v ớ i x ≤ - 2 m x + 3 v ớ i x > - 2
Giá trị nào của m để hàm số đã cho liên tục tại x=-2?
A. 7
B. -7
C. 5
D. 1
Cho hàm số: f x = x 2 - 3 x + 2 x - 2 v ớ i x ≠ 2 m v ớ i x = 2
Với giá trị nào của m thì hàm số đã cho liên tục tại x=2?
A. -2
B. -1
C. 1
D. 3
Cho hàm số f ( x ) = x 2 - 1 x + 1 và f(2) = m2 - 2 với x ≠ 2. Giá trị của m để f(x) liên tục tại x = 2 là:
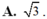
![]()
![]()
![]()
Cho hàm số f ( x ) = x 2 - 1 x + 1 và f ( 2 ) = m 2 - 2 với x ≠ 2. Giá trị của m để f(x) liên tục tại x = 2 là:
A. 3
B. - 3
C. ± 3
D. ± 3
Cho hàm số f ( x ) = x 2 - 1 x + 1 và f ( 2 ) = m 2 - 2 với x ≢ 2 . Giá trị của m để f(x) liên tục tại x =2 là:
A. 3
B. - 3
C. ± 3
D. ± 3
Cho hàm số: f x = 3 x - 5 v ớ i x ≤ - 2 a x - 1 v ớ i x > - 2
Với giá trị nào của a thì hàm số f(x) liên tục tại x=-2?
A. a=-5
B. a=0
C. a=5
D. a=6
Cho hàm số y=f(x) có đạo hàm f'(x) = ( x - 1 ) 2 ( x 2 - 2 x ) với ∀ x ∈ ℝ . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số có 5 điểm cực trị?
A. 15
B. 17
C. 16
D. 18
Tìm giá trị của tham số m để hàm số f ( x ) = x - 1 x 2 - 1 n ế u x ≠ 1 m 2 n ế u x = 1 liên tục tại x = 1
Cho hàm số y = x3 + 3mx2 + (m + 1)x + 1 (1), m là tham số thực. Tìm các giá trị của m để tiếp tuyến của đồ thị của hàm số (1) tại điểm có hoành độ x = -1 đi qua điểm A(1; 2).
A: 1
B: -1
C: 3/4
D: 5/8