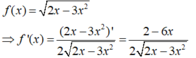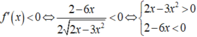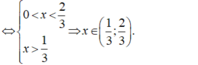Các câu hỏi tương tự
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
Cho hàm số
f
(
x
)
x
3
+
2
x
2
-
7
x
+
3
. Để
f
(
x
)
≤
0
thì x có giá trị thuộc tập hợp nào? A.
-
7
3
;
1
B.
-
1...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + 2 x 2 - 7 x + 3 . Để f ' ( x ) ≤ 0 thì x có giá trị thuộc tập hợp nào?
A. - 7 3 ; 1
B. - 1 ; 7 3
C. - 7 3 ; 1
D. - 7 3 ; 1
Cho hàm số
f
(
x
)
x
3
+
2
x
2
−
7
x
+
3
. Để
f
(
x
)
≤
0
thì x có giá trị thuộc tập hợp nào? A.
−
7
3
;...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + 2 x 2 − 7 x + 3 . Để f ' ( x ) ≤ 0 thì x có giá trị thuộc tập hợp nào?
A. − 7 3 ; 1
B. − 1 ; 7 3
C. − 7 3 ; 1
D. − 7 3 ; 1
Cho hàm số
f
(
x
)
2
x
−
3
x
2
. Để
f
(
x
)
0
thì x có giá trị thuộc tập hợp nào dưới đây? A.
−
∞
;
1
3...
Đọc tiếp
Cho hàm số f ( x ) = 2 x − 3 x 2 . Để f ' ( x ) < 0 thì x có giá trị thuộc tập hợp nào dưới đây?
A. − ∞ ; 1 3
B. 0 ; 1 3
C. 1 3 ; 2 3
D. 1 3 ; + ∞
Câu 1:Cho f(x) dfrac{sqrt{x+2}-sqrt{2-x}}{x}, x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x0?Câu 2:Xét tính liên tục của hàm sốa, f(x) left{{}begin{matrix}x+dfrac{3}{2}dfrac{sqrt{x+1}-1}{sqrt[3]{1+x}-1}end{matrix}right.khi x≤0 và x0 tại xo0b, f(x) left{{}begin{matrix}dfrac{x^3-x^2+2x-2}{x-1}3x+aend{matrix}right.với x1 và với x≥1, xo1
Đọc tiếp
Câu 1:
Cho f(x)= \(\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}\), x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x=0?
Câu 2:
Xét tính liên tục của hàm số
a, f(x)= \(\left\{{}\begin{matrix}x+\dfrac{3}{2}\\\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}\end{matrix}\right.\)khi x≤0 và x>0 tại xo=0
b, f(x)= \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\\3x+a\end{matrix}\right.\)với x<1 và với x≥1, xo=1
Cho hàm số y (2x2 + 1)3. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây? A. ∅. B. (-∞; 0]. C. [0; +∞). D. R
Đọc tiếp
Cho hàm số y = (2x2 + 1)3. Để y’ ≥ 0 thì x nhận các giá trị thuộc tập nào sau đây?
A. ∅.
B. (-∞; 0].
C. [0; +∞).
D. R
1) đạo hàm của hàm số \(\dfrac{2x^2+1}{x^2}\) là
2) cho hàm số \(f\left(x\right)=\sqrt{-5x^2+14x-9}\) tập hợp các giá trị của x để f'(x) = 0 là
Cho hàm số f(x)
2
x
3
+
a
x
2
-
4
x
+
b...
Đọc tiếp
Cho hàm số f(x)= 2 x 3 + a x 2 - 4 x + b ( x - 1 ) 2 k h i x ≠ 1 3 c + 1 k h i x = 1 . Biết rằng a, b, c là giá trị thực để hàm số liên tục tại x 0 = 1 . Giá trị c thuộc khoảng nào sau đây?
A. c ∈ ( 0 ; 1 )
B. c ∈ 1 ; 2
C. c ∈ 2 ; 3
D. c ∈ 3 ; 4
cho hàm số f(x)=\(x^2-4x+3\)
tìm gtri tham số m để \(\left|f\left(\left|x\right|\right)-1\right|=m\) có 8 nghiệm phân biệt
đáp án:
A. \(m< 1\)
B.\(0\le x\le2\)
C.1<x<2
D.0<x<1