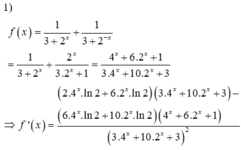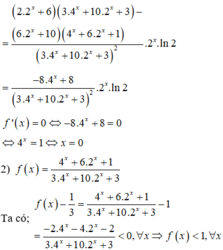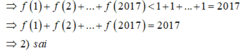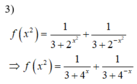Các câu hỏi tương tự
Cho hàm số
f
(
x
)
1
3
+
2
x
+
1
3
+
2
-
x
. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
1
)
f
(
x...
Đọc tiếp
Cho hàm số f ( x ) = 1 3 + 2 x + 1 3 + 2 - x . Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
1 ) f ' ( x ) # 0 , ∀ x ∈ R
2 ) f ( 1 ) + f ( 2 ) + . . . + f ( 2017 ) = 2017
3 ) f ( x 2 ) = 1 3 + 4 x + 1 3 + 4 - x
A. 0
B. 3
C. 2
D. 1
Cho hàm số y f(x) xác định trên
ℝ
và có đồ thị của hàm số
f
(
x
)
,
biết
f
(
3
)
+
f
(
2
)
f...
Đọc tiếp
Cho hàm số y = f(x) xác định trên ℝ và có đồ thị của hàm số f ' ( x ) , biết f ( 3 ) + f ( 2 ) = f ( 0 ) + f ( 1 ) và các khẳng định sau:
Hàm số y = f(x) có 2 điểm cực trị.
Hàm số y = f(x) đồng biến trên khoảng ( - ∞ ; 0 ) .
Max [ 0 ; 3 ] f ( x ) = f ( 3 ) .
Min ℝ f ( x ) = f ( 2 ) .
Max [ - ∞ ; 2 ] f ( x ) = f ( 0 ) .

Số khẳng định đúng là
A. 2.
B. 3.
C. 4.
C. 4.
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f(x), biết f(3)+f(20f(0)+f(1) và các khẳng định sau:1) Hàm số yf(x) có 2 điểm cực trị2) Hàm số yf(x) đồng biến trên khoảng
-
∞
;
0
3)
M
a
x
0
;
3
f...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f'(x), biết f(3)+f(20=f(0)+f(1) và các khẳng định sau:
1) Hàm số y=f(x) có 2 điểm cực trị
2) Hàm số y=f(x) đồng biến trên khoảng - ∞ ; 0
3) M a x 0 ; 3 f x = f 3
4) M a x ℝ f x = f 2
5) M a x - ∞ ; 2 f x = f 0 .
Số khẳng định đúng là

A. 2
B. 3
C. 4
D. 5
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn (
[
f
(
x
)
]
2
[
f
(
x
)
]
2...
Đọc tiếp
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn ( [ f ( x ) ] 2 [ f ' ( x ) ] 2 ) e 2 x = 1 + [ f ( x ) ] 2 và f(x)> 0 với ∀x∈[0;1], biết f(0)=1. hãy chọn khẳng định đúng trong các khẳng định sau
A. 5 2 <f(1)< 3
B. 3<f(1)< 7 2
C. 2<f(1)< 5 2
D. 3 2 <f(1)< 2
Cho hàm số yf(x) xác định trên
ℝ
và có đồ thị của hàm số f’(x) và các khẳng định sau:(1). Hàm số yf(x) đồng biến trên khoảng
1
;
+
∞
(2). Hàm số yf(x) nghịch biến trên khoảng
-
∞
;
-
2
(3). Hàm số yf(x) nghịch biến trên khoảng
-...
Đọc tiếp
Cho hàm số y=f(x) xác định trên ℝ và có đồ thị của hàm số f’(x) và các khẳng định sau:
(1). Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞
(2). Hàm số y=f(x) nghịch biến trên khoảng - ∞ ; - 2
(3). Hàm số y=f(x) nghịch biến trên khoảng - 2 ; 1 .
(4). Hàm số y = f x 2 đồng biến trên khoảng - 1 ; 0
(5). Hàm số y = f x 2 nghịch biến trên khoảng (1;2)

Số khẳng định đúng là
A. 4
B. 3
C. 2
D. 5
Cho hàm số f(x) có đạo hàm trên ℝ và f '(x) > 0, ∀ x ∈ ℝ . Biết f(1)=2. Hỏi khẳng định nào sau đây có thể xảy ra?
A. f(2) + f(3) = 4
B. f(-1) = 2
C. f(2) = 1
D. f(2018) > f(2019)
Cho hàm số
f
x
x
2
-
3
x
-
3
,
x
≠...
Đọc tiếp
Cho hàm số f x = x 2 - 3 x - 3 , x ≠ 3 2 3 , x = 3 . Tìm khẳng định đúng trong các khẳng định sau:
( I ). f(x) liên tục x = 3 .
( II ). f(x) gián đoạn tại x = 3 .
( III ). f(x) liên tục trên ℝ
A. Chỉ ( II ) và ( III ).
B. Chỉ ( I ) và ( III ).
C. Cả ( I ),( II ) và ( III ) đều đúng.
D. Chỉ ( I ) và ( II ).
Cho hàm số
f
(
x
)
liên tục trên
ℝ
và
f
(
x
)
≠
0
với mọi
x
∈
ℝ
thỏa mãn
f
(
x
)
(
2
x
+
1
)
.
f
2
(
x...
Đọc tiếp
Cho hàm số f ( x ) liên tục trên ℝ và f ( x ) ≠ 0 với mọi x ∈ ℝ thỏa mãn f ' ( x ) = ( 2 x + 1 ) . f 2 ( x ) v à f ( 1 ) = - 0 , 5 . Biết tổng f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . + f ( 2017 ) = a b ; ( a ∈ ℝ ; b ∈ ℝ ) v ớ i a b tối giản. Mệnh đề nào dưới đây đúng?
A. b - a = 4035
B. a + b = - 1
C. a b < - 1
D. a ∈ - 2017 ; 2017
Cho hàm số y f (x) có
f
(
x
)
(
2
x
-
1
)
x
2
(
1
-
x
)
2
Khẳng định nào sau đây là khẳng định đúng? A. Hàm số đã cho có đúng một cực trị. B. Hàm số đã cho không có cực trị. C. Hàm số đã cho có hai cực trị. D. Hàm số đã cho có ba cực trị
Đọc tiếp
Cho hàm số y = f (x) có f ' ( x ) = ( 2 x - 1 ) x 2 ( 1 - x ) 2 Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đã cho có đúng một cực trị.
B. Hàm số đã cho không có cực trị.
C. Hàm số đã cho có hai cực trị.
D. Hàm số đã cho có ba cực trị