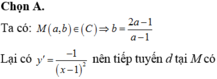Các câu hỏi tương tự
Cho hàm số
y
2
x
-
1
x
-
1
có đồ thị (C) và điểm I(1;2). Điểm M(a;b), a0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM. Giá trị a+b bằng A. 1 B. 2 C. 4 D. 5
Đọc tiếp
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C) và điểm I(1;2). Điểm M(a;b), a>0 thuộc (C) sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM. Giá trị a+b bằng
A. 1
B. 2
C. 4
D. 5
Cho hàm số y = 2 x - 1 x - 1 có đồ thị (C) và điểm I(1;2). Điểm M(a;b) thuộc (C) với sao cho tiếp tuyến tại M của (C) vuông góc với đường thẳng IM. Giá trị của tổng bằng:
A. 1
B. 2
C. 4
D. 5
Cho d là đường thẳng đi qua điểm
A
-
1
;
3
và có hệ số góc m. Gọi S là tập hợp các giá trị của tham số m để đường thẳng d cắt đồ thị
C
của hàm số
y
x
3
-
3
x
+
1
tại ba điểm phân biệt A, B, C sao cho tiếp tuyến với đồ thị tại B và C cắt nhau tại điểm I nằm trên...
Đọc tiếp
Cho d là đường thẳng đi qua điểm A - 1 ; 3 và có hệ số góc m. Gọi S là tập hợp các giá trị của tham số m để đường thẳng d cắt đồ thị C của hàm số y = x 3 - 3 x + 1 tại ba điểm phân biệt A, B, C sao cho tiếp tuyến với đồ thị tại B và C cắt nhau tại điểm I nằm trên đường tròn đường kính BC. Tính tổng bình phương các phần tử thuộc tập hợp S.
A. 16 9
B. 34 9
C. 38 9
D. 34 3
Cho hàm số
y
x
3
-
3
x
+
2
C
. Biết rằng đường thẳng
d
:
y
m
x
+
1
cắt
C
tại ba điểm phân biệt A, B, C. Tiếp tuyến tại ba điểm A, B, C của đồ thị cắt đồ thị
C
lần lượt tại các điểm A, B, C(tương ứng khác A, B, C). Biết rằng A, B, C thẳng hàng, tìm giá trị...
Đọc tiếp
Cho hàm số y = x 3 - 3 x + 2 C . Biết rằng đường thẳng d : y = m x + 1 cắt C tại ba điểm phân biệt A, B, C. Tiếp tuyến tại ba điểm A, B, C của đồ thị cắt đồ thị C lần lượt tại các điểm A', B', C'(tương ứng khác A, B, C). Biết rằng A', B', C' thẳng hàng, tìm giá trị của tham số m để đường thẳng đi qua ba điểm A', B', C' vuông góc với đường thẳng ∆ : x + 2018 y - 2019 = 0
A. m = 1009 2
B. m = 1009 4
C. m = 2009 4
D. m = 2019 4
Cho hàm số
y
x
4
-
2
(
m
+
1
)
x
2
+
m
+
2
có đồ thị (C) . Gọi
∆
là tiếp tuyến với đồ thị (C) tại điểm thuộc (C) có hoành độ bằng 1. Với giá trị nào của tham số m thì
∆
vuông góc với đường thẳng d:
y
-
1
4
x
-
2016
A. m-1 B. m0 C. m1 D. m2
Đọc tiếp
Cho hàm số y = x 4 - 2 ( m + 1 ) x 2 + m + 2 có đồ thị (C) . Gọi ∆ là tiếp tuyến với đồ thị (C) tại điểm thuộc (C) có hoành độ bằng 1. Với giá trị nào của tham số m thì ∆ vuông góc với đường thẳng d: y = - 1 4 x - 2016
A. m=-1
B. m=0
C. m=1
D. m=2
Gọi S là tập hợp tất cả các giá trị thực của a sao cho đường thẳng ya(x-1)-3 cắt đồ thị (C) của hàm số
y
2
x
3
-
3
x
2
-
2
tại ba điểm M,N,P(1;-3) và tiếp tuyến của (C) tại M,N vuông góc với nhau. Tổng các phần tử của S bằng A. -1. B. 1. C. 2. D. -2
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của a sao cho đường thẳng y=a(x-1)-3 cắt đồ thị (C) của hàm số y = 2 x 3 - 3 x 2 - 2 tại ba điểm M,N,P(1;-3) và tiếp tuyến của (C) tại M,N vuông góc với nhau. Tổng các phần tử của S bằng
A. -1.
B. 1.
C. 2.
D. -2
Cho hàm số
y
−
x
+
1
2
x
−
1
có đồ thị là (C), đường thẳng
d
:
y
x
+
m
. Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi
k
1
,
k
2...
Đọc tiếp
Cho hàm số y = − x + 1 2 x − 1 có đồ thị là (C), đường thẳng d : y = x + m . Với mọi m ta luôn có d cắt (C) tại 2 điểm phân biệt A, B. Gọi k 1 , k 2 lần lượt là hệ số góc của các tiếp tuyến với (C) tại A, B. Tìm m để tổng k 1 + k 2 đạt giá trị lớn nhất.
A. m = -1
B. m = -2
C. m = 3
D. m = -5
Cho hàm số
y
x
3
-
3
x
có đồ thị (C). Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng
d
:
y
k
(
x
+
1
)
+
2
cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M (-1;2), tính tích tất cả các phần tử của tập S A....
Đọc tiếp
Cho hàm số y = x 3 - 3 x có đồ thị (C). Gọi S là tập hợp tất cả các giá trị thực của k để đường thẳng d : y = k ( x + 1 ) + 2 cắt đồ thị (C) tại ba điểm phân biệt M, N, P sao cho các tiếp tuyến của (C) tại N và P vuông góc với nhau. Biết M (-1;2), tính tích tất cả các phần tử của tập S
A. 1 9
B. - 2 9
C. 1 3
D. -1
Cho hàm số
y
x
+
b
a
x
−
2
có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm
M
1
;
−
2
song song với đường thẳng
3
x
+
y
−
4...
Đọc tiếp
Cho hàm số y = x + b a x − 2 có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm M 1 ; − 2 song song với đường thẳng 3 x + y − 4 = 0. Khi đó tổng giá trị của a + b bằng:
A. 2
B. 1
C. -1
D. 0