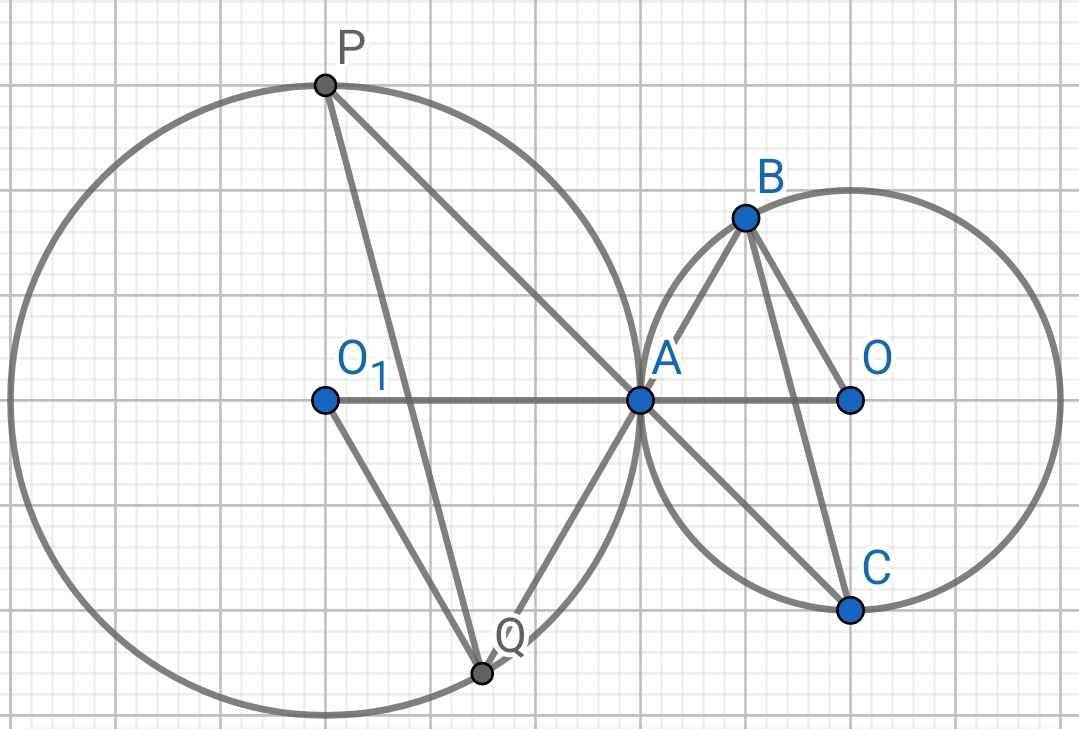
∆O₁AQ có:
O₁A = O₁Q (bán kính)
⇒ ∆O₁AQ cân tại O₁
⇒ ∠O₁AQ = ∠O₁QA (1)
∆OAB có:
OA = OB (bán kính)
⇒ ∆OAB cân tại O
⇒ ∠OAB = ∠OBA (2)
Mà ∠OAB = ∠O₁AQ (đối đỉnh)
⇒ ∠OBA = ∠O₁AQ (3)
Từ (1), (2) và (3) ⇒ ∠AO₁Q = ∠AOB
Trong (O₁) có:
∠APQ = ∠AO₁Q : 2 (góc nội tiếp và góc ở tâm cùng chắn cung AQ) (4)
Trong (O) có:
∠ACB = ∠AOB : 2 (góc nội tiếp và góc ở tâm cùng chắn cung AB) (5)
Mà ∠AO₁Q = ∠AOB (cmt) (6)
Từ (4), (5) và (6) ⇒ ∠APQ = ∠ACB
Mà ∠APQ và ∠ACB là hai góc so le trong
⇒ PQ // BC












