Các câu hỏi tương tự
Trong mặt phẳng tọa độ Oxy, cho điểm K(1;1) và đường thẳng (Δ) có phương trình \(y=2x+\sqrt{3}\). Gọi (d) là 1 đường thẳng song song với đường thẳng (Δ) có và cắt trục tung tại điểm có tung độ bằng 1. Hãy tính khoảng cách từ K đến đường thẳng (d)
Hai đường thẳng y = x + 3 và y = 2x + 3 trên cùng một mặt phẳng tọa độ có vị trí tương đối là:
A. Trùng nhau
B. Cắt nhau tại điểm có tung độ 3
C. Song song
D. Cắt nhau tại điểm có hoành độ là 3
a) Vẽ đồ thị của các hàm số y x và y 2x trên cùng một mặt phẳng tọa độ Oxy (hình 5).b) Đường thẳng song song với trục Ox và cắt trục Oy tại các điểm có tung độ y 4 lần lượt cắt các đường thẳng y 2x, y x tại hai điểm A và B.Tìm tọa độ các điểm A, B, tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimetHình 5
Đọc tiếp
a) Vẽ đồ thị của các hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy (hình 5).
b) Đường thẳng song song với trục Ox và cắt trục Oy tại các điểm có tung độ y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại hai điểm A và B.
Tìm tọa độ các điểm A, B, tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là xentimet
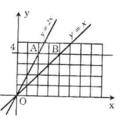
Hình 5
cho hàm số y=mx+n-3x (d).Xác định m,n để đường thẳng (d)
a, đi qua điểm A(1,-3);B(-2,3)
b,Cắt trục tung tại điểm có tung độ bằng 1-\(\sqrt{3}\),cắt trục hoành tại điểm có hoành độ bằng 3+\(\sqrt{3}\)
c,cắt đường thẳng 3y-x-4=0
d,song song với đường thẳng 2x+5y=-1
1) Ba đường thẳng ysqrt{2}x, y frac{1}{2}x, y 2 cắt nhau tạo thành một tam giác. Tính diện tích tam giác đó.2) Trong mặt phẳng tọa độ, cho đa giác OABCDE (không lồi ) có tọa độ A(0;3), B(3;3), C(3;1), D(5;1), E(5;0). Tìm hệ số a sao cho đường thẳng yax chia đa giác thành hai phần có diện tích bằng nhau.3) Xác định các số nguyên a,b sao cho đường thẳng yax +b đi qua điểm A(4;3), cắt trục tung, trục hoành tại điểm có tung độ, hoành độ là một số nguyên dương.
Đọc tiếp
1) Ba đường thẳng y=\(\sqrt{2}\)x, y= \(\frac{1}{2}\)x, y= 2 cắt nhau tạo thành một tam giác. Tính diện tích tam giác đó.
2) Trong mặt phẳng tọa độ, cho đa giác OABCDE (không lồi ) có tọa độ A(0;3), B(3;3), C(3;1), D(5;1), E(5;0). Tìm hệ số a sao cho đường thẳng y=ax chia đa giác thành hai phần có diện tích bằng nhau.
3) Xác định các số nguyên a,b sao cho đường thẳng y=ax +b đi qua điểm A(4;3), cắt trục tung, trục hoành tại điểm có tung độ, hoành độ là một số nguyên dương.
1/Xác định hàm số bậc nhất y=ax+b biết đồ thị của nó song song với đường thẳng y=2x-3 và cắt trục tung tại điểm có tung độ bằng 5
2/ a.Vẽ trên cùng mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:y=-2x+5(d1) ; y=x+2(d2)
b. Tìm tọa độ giao điểm M của hai đường thẳng (d1) và (d2)
c. Tính góc αα tạo bởi đường thẳng (d2) và trục hoành Ox
Viết phương trình đường thẳng thỏa mãn một trong các điều kiện sau:
a, Đi qua điểm A (2;2) bà B(1;3)
b.Cắt trục tung tại điểm có tung độ bằng 3 và cắt trục hoành tại điểm có hoành độ bằng \(\sqrt{2}\)
c. Song song với đường thẳng y=3x + 1 và đi qua điểm M(4:-5)
Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y = x2 và đường thẳng (d): y = mx - m + 1
Tìm m để (d) và (P) cắt nhau tại 2 điểm phân biệt có hoành độ x1, x2 là độ dài hai cạnh góc vuông của 1 tam giác vuông có độ dài đường cao tương ứng với cạnh huyền bằng \(\frac{1}{\sqrt{5}}\)
Trong mặt phẳng tọa độ Ãy cho parapol (P): y=\(x^2\) và đường thẳng (d): y=mx+1-m.
a) Xác định tọa độ giao điểm của (P) và (d) khi m=-1
b) Tìm m để (P) và (d) cắt nhau tại 2 điểm phân biệt có hoàng độ \(x_1\);\(x_2\) thỏa mãn \(\sqrt{x_1}+\sqrt{x_2}=3\)













