Đáp án B
Ta có: f x + f 1 − x = 1 .
Suy ra S = f 1 2017 + f 2 2017 + ... + f 2016 2017
= 2016 2 f x + f 1 − x = 1008.
Đúng 0
Bình luận (0)
Các câu hỏi tương tự
Cho biểu thức
f
x
1
2018
x
+
2018
.
Tính tổng sau
S
2018
[
f
−
2017
+
f
−
2016
+
...
+
f...
Đọc tiếp
Cho biểu thức f x = 1 2018 x + 2018 . Tính tổng sau
S = 2018 [ f − 2017 + f − 2016 + ... + f 0 + f 1 + ... + f 2018 ]
A. S = 2018
B. S = 1 2018
C. S = 2018
D. S = 1 2018
Cho biểu thức
f
x
1
2018
x
+
2018
.
Tính tổng
S
2018
f
−
2017
+
f
−
2016...
Đọc tiếp
Cho biểu thức f x = 1 2018 x + 2018 .
Tính tổng S = 2018 f − 2017 + f − 2016 + ... + f 0 + f 1 + ... + f 2018 .
A. S = 2018
B. S = 1 2018
C. S = 2018
D. S = 1 2018
Cho f(x)
x
x
2
+
1
(
2
x
2
+
1
+
2017
)
, biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)2018. Tính F(2) A. F(2) 5+2017
5
B. F(2) 4+2017
4
C. F(2) 3+2017
3...
Đọc tiếp
Cho f(x)= x x 2 + 1 ( 2 x 2 + 1 + 2017 ) , biết F(x) là một nguyên hàm của f(x) thỏa mãn F(0)=2018. Tính F(2)
A. F(2) = 5+2017 5
B. F(2) = 4+2017 4
C. F(2) = 3+2017 3
D. F(2)= 2022
Gọi F(x) là một nguyên hàm của hàm số f (x)
2
x
thỏa mãn
F
(
0
)
1
ln
2
. Tính giá trị biểu thức
T
F
(
0
)
+
F
(
1
)
+
F
(
2
)
+
.
.
.
+
F
(
2017
)
. A.
T
1009
....
Đọc tiếp
Gọi F(x) là một nguyên hàm của hàm số f (x)= 2 x thỏa mãn F ( 0 ) = 1 ln 2 . Tính giá trị biểu thức T = F ( 0 ) + F ( 1 ) + F ( 2 ) + . . . + F ( 2017 ) .
A. T = 1009 . 2 2017 + 1 ln 2
B. T = 2 2017 . 2018
C. T = 2 2017 - 1 ln 2
D. T = 2 2018 - 1 ln 2
Cho hàm số y = f(x) = ax4 + bx2 + c biết a > 0, c > 2017 và a + b + c < 2017. Số cực trị của hàm số y = |f(x) – 2017| là
A. 1
B. 3
C. 7
D. 5
Giá trị của
A
1
1
!
.2018
!
+
1
2
!
.2017
!
+
1
3
!
.2016
!
+
...
+...
Đọc tiếp
Giá trị của
A = 1 1 ! .2018 ! + 1 2 ! .2017 ! + 1 3 ! .2016 ! + ... + 1 1008 ! .1011 ! + 1 1009 ! .1010 ! bằng
A. 2 2017 − 1 2018 ! .
B. 2 2017 2018 ! .
C. 2 2017 2019 ! .
D. 2 2018 − 1 2019 ! .
Cho hàm số
y
f
(
x
)
2019
l
n
e
x
2019
+
e
. Tính giá trị biểu thức
A
f
’
(
1
)
+...
Đọc tiếp
Cho hàm số y = f ( x ) = 2019 l n e x 2019 + e . Tính giá trị biểu thức A = f ’ ( 1 ) + f ’ ( 2 ) + … + f ’ ( 2018 )
A. 2018
B. 1009
C. 2017 2
D. 2019 2
Cho hàm số
y
f
x
có đạo hàm cấp hai trên R. Biết
f
0
3
;
f
2
-
2018
và bảng xét dấu của
f
0
như sau:Hàm số
y
f
x
+
2017...
Đọc tiếp
Cho hàm số y = f x có đạo hàm cấp hai trên R. Biết f ' 0 = 3 ; f ' 2 = - 2018 và bảng xét dấu của f ' ' 0 như sau:
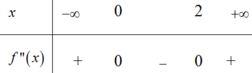
Hàm số y = f x + 2017 + 2018 x đạt giá trị nhỏ nhất tại điểm x 0 thuộc khoảng nào sau đây?
A. 0 ; 2
B. - ∞ ; - 2017
C. - 2017 ; 0
D. 2017 ; + ∞
Cho hàm số
f
(
x
)
a
x
4
+
b
x
2
+
c
với
a
0
,
c
2017
và
a
+
b
+
c
2017
. Số cực trị của hàm số
y
f
x
-
2017
là A. 1 B. 5 C. 3 D. 7
Đọc tiếp
Cho hàm số f ( x ) = a x 4 + b x 2 + c với a > 0 , c > 2017 và a + b + c < 2017 . Số cực trị của hàm số y = f x - 2017 là
A. 1
B. 5
C. 3
D. 7
Cho hàm số
y
f
x
2018
ln
e
x
2018
+
e
.
Tính giá trị biểu thức
T
f
1
+
f
2
+
...
+
f
2017...
Đọc tiếp
Cho hàm số y = f x = 2018 ln e x 2018 + e . Tính giá trị biểu thức T = f ' 1 + f ' 2 + ... + f ' 2017 .
A. T = 2019 2
B. T = 1009
C. T = 2017 2
D. T = 1008