Đáp án D.
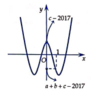
Xét hàm số g ( x ) = f ( x ) - 2017 = a x 4 + b x 2 + c - 2017 là hàm trùng phương nên đồ thị hàm số nhận trục Oy làm trục đối xứng và luôn nhận x = 0 là một điểm cực trị.
Ta có g ( 0 ) = c - 2017 > 0 ( d o x > 2017 ) g ( 1 ) = a + b + c - 2107 < 0 ( d o a + b + c < 2017 ) ⇒ g ( 0 ) . g ( 1 ) < 0 ⇒ phương trình g ( x ) = 0 có nghiệm ( 0 ; 1 ) .
Lại có lim x → + ∞ g ( x ) = lim x → + ∞ = x 4 a + b x 2 + c - 2017 x 4 = + ∞ ( d o a > 0 ) nên tồn tại x = x 0 đủ lớn ( x 0 → + ∞ ) sao cho g ( x 0 ) > 0 ⇒ g ( 1 ) . g ( x 0 < 0 ⇒ ) phương trình g ( x ) = 0 có nghiệm trên 1 ; + ∞ .
Như vậy, với x > 0 thì phương trình g (x) =0 có ít nhất hai nghiệm nên đồ thị hàm số g (x) cắt Ox tại ít nhất hai điểm nằm bên phải trục tung. Suy ra phương trình g (x) có đúng 4 nghiệm hay đồ thị hàm số g(x) cắt Ox tại đúng 4 điểm và có đồ thị như hình bên. Suy ra hàm số y = g(x) có 3 điểm cực trị (1 cực đại, 2 cực tiểu).
Khi đó hàm số y = g ( x ) có 3 + 4 = 7 điểm cực trị.



