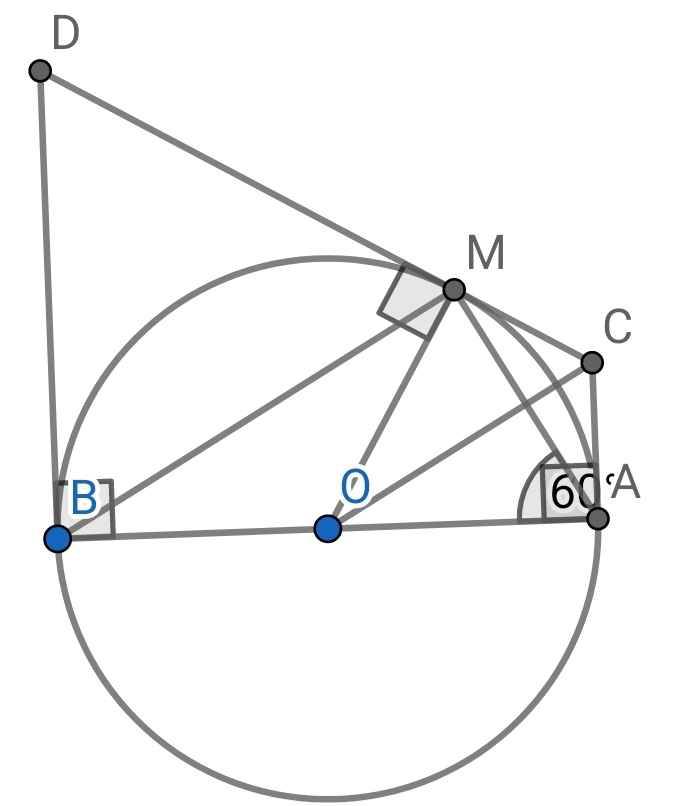
a) Do AC là tiếp tuyến tại A của (O) (gt)
⇒ ∠CAO = 90⁰
Do MC là tiếp tuyến tại M của (O) (gt)
⇒ ∠CMO = 90⁰
Tứ giác AOMC có:
∠CAO + ∠MAO = 90⁰ + 90⁰ = 180⁰
⇒ AOMC nội tiếp
b) ∆OAM có:
OA = OM (bán kính)
⇒ ∆OAM cân tại O
Mà ∠OAM = ∠BAM = 60⁰ (gt)
⇒ ∆OAM là tam giác đều
⇒ ∠AOM = 60⁰
Do AOMC nội tiếp (cmt)
⇒ ∠AOM + ∠ACM = 180⁰ (hai góc đối của tứ giác nội tiếp AOMC)
⇒ ∠ACM = 180⁰ - ∠AOM
= 180⁰ - 60⁰
= 120⁰
Do AC và MC là hai tiếp tuyến của (O) cắt nhau tại C
⇒ CO là tia phân giác của ∠ACM
⇒ ∠OCM = ∠ACM : 2
= 120⁰ : 2
= 60⁰ (1)
Do ∠BMD và ∠BAM là góc tạo bởi tia tiếp tuyến MD và góc nội tiếp cùng chắn cung BM
⇒ ∠BMD = ∠BAM = 60⁰ (2)
Từ (1) và (2) ⇒ ∠BMD = ∠OCM = 60⁰
Mà ∠BMD và ∠OCM là hai góc đồng vị
⇒ OC // BM












